
【題目】已知在△ABC中,角A,B,C的對(duì)邊分別為a,b,c,且 ![]() +
+ ![]() =
= ![]() .
.
(1)求b的值;
(2)若cosB+ ![]() sinB=2,求a+c的取值范圍.
sinB=2,求a+c的取值范圍.
【答案】
(1)解:△ABC中, ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得b= ![]() ;
;
(2)解:∵cosB+ ![]() sinB=2,
sinB=2,
∴cosB=2﹣ ![]() sinB,
sinB,
∴sin2B+cos2B=sin2B+ ![]() =4sin2B﹣4
=4sin2B﹣4 ![]() sinB+4=1,
sinB+4=1,
∴4sin2B﹣4 ![]() sinB+3=0,
sinB+3=0,
解得sinB= ![]() ;
;
從而求得cosB= ![]() ,
,
∴B= ![]() ;
;
由正弦定理得 ![]() =
= ![]() =
= ![]() =
= ![]() =1,
=1,
∴a=sinA,c=sinC;
由A+B+C=π得A+C= ![]() ,
,
∴C= ![]() ﹣A,且0<A<
﹣A,且0<A< ![]() ;
;
∴a+c=sinA+sinC
=sinA+sin( ![]() ﹣A)
﹣A)
=sinA+sin ![]() cosA﹣cos
cosA﹣cos ![]() sinA
sinA
= ![]() sinA+
sinA+ ![]() cosA
cosA
= ![]() sin(A+
sin(A+ ![]() ),
),
∵0<A< ![]() ,∴
,∴ ![]() <A+
<A+ ![]() <
< ![]() ,
,
∴ ![]() <sin(A+
<sin(A+ ![]() )≤1,
)≤1,
∴ ![]() <
< ![]() sin(A+
sin(A+ ![]() )≤
)≤ ![]() ,
,
∴a+c的取值范圍是( ![]() ,
, ![]() ].
].
【解析】(1)應(yīng)用正弦、余弦定理化簡(jiǎn) ![]() +
+ ![]() =
= ![]() ,即可求出b的值;(2)根據(jù)cosB+
,即可求出b的值;(2)根據(jù)cosB+ ![]() sinB=2與平方關(guān)系sin2B+cos2B=1,求得sinB、cosB,從而求得B的值,再由正弦定理求得a=sinA,c=sinC;利用A+B+C=π求得C=
sinB=2與平方關(guān)系sin2B+cos2B=1,求得sinB、cosB,從而求得B的值,再由正弦定理求得a=sinA,c=sinC;利用A+B+C=π求得C= ![]() ﹣A,且0<A<
﹣A,且0<A< ![]() ;
;
再利用三角恒等變換求a+c=sinA+sinC的取值范圍.
【考點(diǎn)精析】本題主要考查了正弦定理的定義的相關(guān)知識(shí)點(diǎn),需要掌握正弦定理:![]() 才能正確解答此題.
才能正確解答此題.


 浙大優(yōu)學(xué)小學(xué)年級(jí)銜接捷徑浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級(jí)銜接捷徑浙江大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù) ![]() 的定義域是( )
的定義域是( )
A.[﹣2,2]
B.(﹣∞,﹣2]∪[2,+∞)
C.(﹣2,2)
D.(﹣∞,﹣2)∪(2,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是函數(shù) ![]() 圖象的一部分.為了得到這個(gè)函數(shù)的圖象,只要將y=sinx(x∈R)的圖象上所有的點(diǎn)( )
圖象的一部分.為了得到這個(gè)函數(shù)的圖象,只要將y=sinx(x∈R)的圖象上所有的點(diǎn)( )
A.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來(lái)的
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來(lái)的 ![]() ,縱坐標(biāo)不變
,縱坐標(biāo)不變
B.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來(lái)的2倍,縱坐標(biāo)不變
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來(lái)的2倍,縱坐標(biāo)不變
C.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來(lái)的
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來(lái)的 ![]() ,縱坐標(biāo)不變
,縱坐標(biāo)不變
D.向左平移 ![]() 個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來(lái)的2倍,縱坐標(biāo)不變
個(gè)單位長(zhǎng)度,再把所得各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來(lái)的2倍,縱坐標(biāo)不變
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在區(qū)間[0,1]內(nèi)隨機(jī)取兩個(gè)數(shù)分別為a,b,則使得方程x2+2ax+b2=0有實(shí)根的概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】將圓 ![]() 為參數(shù))上的每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉?lái)的
為參數(shù))上的每一點(diǎn)的橫坐標(biāo)保持不變,縱坐標(biāo)變?yōu)樵瓉?lái)的 ![]() 倍,得到曲線C.
倍,得到曲線C.
(1)求出C的普通方程;
(2)設(shè)直線l:x+2y﹣2=0與C的交點(diǎn)為P1 , P2 , 以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系, 求過(guò)線段P1P2的中點(diǎn)且與l垂直的直線的極坐標(biāo)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)f(x)=Asin(ωx+φ)(ω>0, ![]() )的部分圖象如圖所示,將函數(shù)f(x)的圖象向右平移
)的部分圖象如圖所示,將函數(shù)f(x)的圖象向右平移 ![]() 個(gè)單位后得到函數(shù)g(x)的圖象,若函數(shù)g(x)在區(qū)間
個(gè)單位后得到函數(shù)g(x)的圖象,若函數(shù)g(x)在區(qū)間 ![]() (
( ![]() )上的值域?yàn)閇﹣1,2],則θ= .
)上的值域?yàn)閇﹣1,2],則θ= . 
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)f(x)是定義在R上周期為2的奇函數(shù),當(dāng)0≤x≤1時(shí),f(x)=x2﹣x,則 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】北宋數(shù)學(xué)家沈括的主要數(shù)學(xué)成就之一為隙積術(shù),所謂隙積,即“積之有隙”者,如累棋、層壇之類(lèi),這種長(zhǎng)方臺(tái)形狀的物體垛積.設(shè)隙積共n層,上底由長(zhǎng)為a個(gè)物體,寬為b個(gè)物體組成,以下各層的長(zhǎng)、寬依次各增加一個(gè)物體,最下層成為長(zhǎng)為c個(gè)物體,寬為d個(gè)物體組成,沈括給出求隙積中物體總數(shù)的公式為S= ![]() .已知由若干個(gè)相同小球粘黏組成的幾何體垛積的三視圖如圖所示,則該垛積中所有小球的個(gè)數(shù)為 .
.已知由若干個(gè)相同小球粘黏組成的幾何體垛積的三視圖如圖所示,則該垛積中所有小球的個(gè)數(shù)為 . 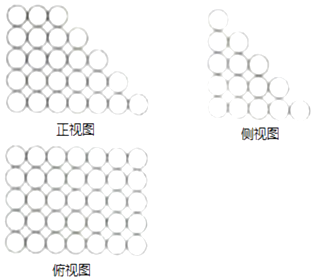
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中,已知點(diǎn)P(2,0),曲線C的參數(shù)方程為 ![]() (t為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系. (Ⅰ)求曲線C的普通方程和極坐標(biāo)方程;
(t為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系. (Ⅰ)求曲線C的普通方程和極坐標(biāo)方程;
(Ⅱ)過(guò)點(diǎn)P且傾斜角為 ![]() 的直線l交曲線C于A,B兩點(diǎn),求|AB|.
的直線l交曲線C于A,B兩點(diǎn),求|AB|.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com