
【題目】已知函數(shù)![]() ,給出下列結論:
,給出下列結論:
①![]() 在
在![]() 上是減函數(shù);
上是減函數(shù);
②![]() 在
在![]() 上的最小值為
上的最小值為![]() ;
;
③![]() 在
在![]() 上至少有兩個零點.
上至少有兩個零點.
其中正確結論的序號為_________(寫出所有正確結論的序號)
【答案】①③
【解析】
根據(jù)y![]() 和y=cosx的單調(diào)性判斷①,②,根據(jù)函數(shù)圖象判斷③.
和y=cosx的單調(diào)性判斷①,②,根據(jù)函數(shù)圖象判斷③.
∵y![]() 和y=cosx在(0,
和y=cosx在(0,![]() )上都是減函數(shù),
)上都是減函數(shù),
∴f(x)在(0,![]() )上是減函數(shù),故①正確;
)上是減函數(shù),故①正確;
同理可得f(x)在(0,π)上是減函數(shù),因為是開區(qū)間,故而f(x)在(0,π)上沒有最小值,故②錯誤;
令f(x)=0可得cosx![]() ,當
,當![]() 時,余弦函數(shù)的函數(shù)值為:
時,余弦函數(shù)的函數(shù)值為:![]()
反比例的函數(shù)值為:![]() ,
,
進而作出y=cosx與y![]() 在(0,2π)上的函數(shù)圖象如圖所示:
在(0,2π)上的函數(shù)圖象如圖所示:
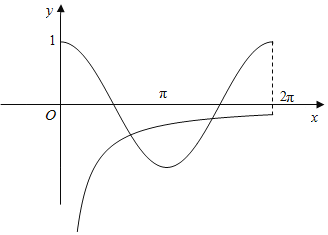
由圖象可知兩函數(shù)在(0,2π)上有2個交點,故f(x)在(0,2π)上有2個零點,故而③正確.
故答案為:①③.


科目:高中數(shù)學 來源: 題型:
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() .
.
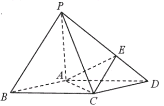
(1)證明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使三棱錐
,使三棱錐![]() 是正三棱錐?證明你的結論.
是正三棱錐?證明你的結論.
(3)求以![]() 為棱,
為棱,![]() 與
與![]() 為面的二面角
為面的二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】過拋物線![]() (其中
(其中![]() )的焦點
)的焦點![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,且
兩點,且![]() 兩點的縱坐標之積為
兩點的縱坐標之積為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)當![]() 時,求
時,求![]() 的值;
的值;
(3)對于![]() 軸上給定的點
軸上給定的點![]() (其中
(其中![]() ),若過點
),若過點![]() 和
和![]() 兩點的直線交拋物線
兩點的直線交拋物線![]() 的準線
的準線![]() 點,求證:直線
點,求證:直線![]() 與
與![]() 軸交于一定點.
軸交于一定點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知橢圓![]() ,直線
,直線![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,點
,點![]() 和點
和點![]() 關于
關于![]() 軸對稱,直線
軸對稱,直線![]() 與
與![]() 軸交于點
軸交于點![]() .
.

(1)若點![]() 是橢圓
是橢圓![]() 的一個焦點,求該橢圓的長軸的長度;
的一個焦點,求該橢圓的長軸的長度;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某書店剛剛上市了《中國古代數(shù)學史》,銷售前該書店擬定了5種單價進行試銷,每本單價(![]() 元)試銷l天,得到如表單價
元)試銷l天,得到如表單價![]() (元)與銷量
(元)與銷量![]() (冊)數(shù)據(jù):
(冊)數(shù)據(jù):
單價 |
|
|
|
|
|
銷量 |
|
|
|
|
|
(1)已知銷量![]() 與單價
與單價![]() 具有線性相關關系,求
具有線性相關關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若該書每本的成本為![]() 元,要使得售賣時利潤最大,請利用所求的線性相關關系確定單價應該定為多少元?(結果保留到整數(shù))
元,要使得售賣時利潤最大,請利用所求的線性相關關系確定單價應該定為多少元?(結果保留到整數(shù))
附:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: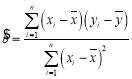
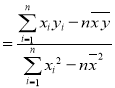 ,
,![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com