
【題目】已知函數(shù)![]() ,其中實(shí)數(shù)
,其中實(shí)數(shù)![]() 為常數(shù),
為常數(shù),![]() 為自然對(duì)數(shù)的底數(shù).
為自然對(duì)數(shù)的底數(shù).
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時(shí),解關(guān)于
時(shí),解關(guān)于![]() 的不等式
的不等式![]() ;
;
(3)當(dāng)![]() 時(shí),如果函數(shù)
時(shí),如果函數(shù)![]() 不存在極值點(diǎn),求
不存在極值點(diǎn),求![]() 的取值范圍.
的取值范圍.
【答案】(1)單調(diào)遞增區(qū)間為![]() ;單調(diào)遞減區(qū)間為
;單調(diào)遞減區(qū)間為![]() .(2)
.(2)![]() (3)
(3)![]()
【解析】試題分析:把![]() 代入由于對(duì)數(shù)的真數(shù)為正數(shù),函數(shù)定義域?yàn)?/span>
代入由于對(duì)數(shù)的真數(shù)為正數(shù),函數(shù)定義域?yàn)?/span>![]() ,所以函數(shù)化為
,所以函數(shù)化為![]() ,求導(dǎo)后在定義域下研究函數(shù)的單調(diào)性給出單調(diào)區(qū)間;代入
,求導(dǎo)后在定義域下研究函數(shù)的單調(diào)性給出單調(diào)區(qū)間;代入![]() ,
,![]() ,分
,分![]() 和
和![]() 兩種情況解不等式;當(dāng)
兩種情況解不等式;當(dāng)![]() 時(shí),
時(shí),![]() ,求導(dǎo)
,求導(dǎo)![]() ,函數(shù)
,函數(shù)![]() 不存在極值點(diǎn),只需
不存在極值點(diǎn),只需![]() 恒成立,根據(jù)這個(gè)要求得出
恒成立,根據(jù)這個(gè)要求得出![]() 的范圍.
的范圍.
試題解析:
(1)![]() 時(shí),
時(shí),![]() ,
,
令![]() ,解得
,解得![]() ,
,
且![]() 時(shí),
時(shí),![]() ,
,![]() 單調(diào)遞減;
單調(diào)遞減;
![]() 時(shí),
時(shí),![]() ,
,![]() 單調(diào)遞增.
單調(diào)遞增.
所以![]() 單調(diào)遞增區(qū)間為
單調(diào)遞增區(qū)間為![]() ;單調(diào)遞減區(qū)間為
;單調(diào)遞減區(qū)間為![]() .
.
(2)![]() 時(shí),
時(shí),![]() .
.
當(dāng)![]() 時(shí),原不等式可化為
時(shí),原不等式可化為![]() .
.
記![]() ,則
,則![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
所以![]() 在
在![]() 單調(diào)遞增,又
單調(diào)遞增,又![]() ,故不等式解為
,故不等式解為![]() ;
;
當(dāng)![]() 時(shí),原不等式可化為
時(shí),原不等式可化為![]() ,顯然不成立,
,顯然不成立,
綜上,原不等式的解集為![]() .
.
(3)![]() 時(shí),
時(shí),![]() ,
,
![]() ,記
,記![]() ,
,
因?yàn)?/span>![]() 時(shí),
時(shí),![]() ,
,
所以![]() 不存在極值點(diǎn)時(shí)
不存在極值點(diǎn)時(shí)![]() 恒成立.
恒成立.
由![]() ,解得
,解得![]()
且時(shí),
![]() ,
,![]() 單調(diào)遞減;
單調(diào)遞減;
![]() 時(shí),
時(shí),![]() ,
,![]() 單調(diào)遞增.
單調(diào)遞增.
所以![]() ,解得
,解得![]() .
.


 周周清檢測(cè)系列答案
周周清檢測(cè)系列答案 輕巧奪冠周測(cè)月考直通高考系列答案
輕巧奪冠周測(cè)月考直通高考系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列![]() 滿足對(duì)任意的
滿足對(duì)任意的![]() 都有
都有![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)數(shù)列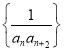 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,不等式
,不等式![]() 對(duì)任意的正整數(shù)
對(duì)任意的正整數(shù)![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】袋子里有編號(hào)為![]() 的五個(gè)球,某位教師從袋中任取兩個(gè)不同的球. 教師把所取兩球編號(hào)的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個(gè)球的編號(hào).
的五個(gè)球,某位教師從袋中任取兩個(gè)不同的球. 教師把所取兩球編號(hào)的和只告訴甲,其乘積只告訴乙,讓甲、乙分別推斷這兩個(gè)球的編號(hào).
甲說(shuō):“我無(wú)法確定.”
乙說(shuō):“我也無(wú)法確定.”
甲聽(tīng)完乙的回答以后,甲又說(shuō):“我可以確定了.”
根據(jù)以上信息, 你可以推斷出抽取的兩球中
A. 一定有3號(hào)球 B. 一定沒(méi)有3號(hào)球 C. 可能有5號(hào)球 D. 可能有6號(hào)球
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】先閱讀下列結(jié)論的證法,再解決后面的問(wèn)題:已知a1 , a2∈R,a1+a2=1,求證a12+a22≥ ![]() .
.
【證明】構(gòu)造函數(shù)f(x)=(x﹣a1)2+(x﹣a2)2
則f(x)=2x2﹣2(a1+a2)x+a12+a22
=2x2﹣2x+a12+a22
因?yàn)閷?duì)一切x∈R,恒有f(x)≥0.
所以△=4﹣8(a12+a22)≤0,從而得a12+a22≥ ![]() ,
,
(1)若a1 , a2 , …,an∈R,a1+a2+…+an=1,請(qǐng)寫(xiě)出上述結(jié)論的推廣式;
(2)參考上述解法,對(duì)你推廣的結(jié)論加以證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分圖象如圖所示.
)的部分圖象如圖所示. 
(1)求函數(shù)的解析式;
(2)設(shè) ![]() π<x<
π<x< ![]() π,且方程f(x)=m有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍和這兩個(gè)根的和.
π,且方程f(x)=m有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍和這兩個(gè)根的和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知y=f(x)是R上的可導(dǎo)函數(shù),對(duì)于任意的正實(shí)數(shù)t,都有函數(shù)g(x)=f(x+t)﹣f(x)在其定義域內(nèi)為減函數(shù),則函數(shù)y=f(x)的圖象可能為如圖中( )
A.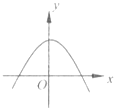
B.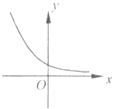
C.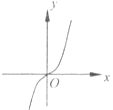
D.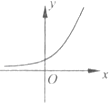
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知平面內(nèi)有三個(gè)向量 ![]() ,其中∠AOB=60°,∠AOC=30°,且
,其中∠AOB=60°,∠AOC=30°,且 ![]() ,
, ![]() ,
, ![]() ,若
,若 ![]() ,則λ+μ= .
,則λ+μ= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱錐![]() 中,
中, ![]() ,
, ![]() 分別為線段
分別為線段![]() 上的點(diǎn),且
上的點(diǎn),且![]() ,
,
![]() .
.

(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com