
【題目】已知![]() 為
為![]() 的三個內角,且其對邊分別為
的三個內角,且其對邊分別為![]() ,若
,若![]() .
.
(1)求角![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)先由正弦定理得![]() ,再根據特殊角三角函數值得角
,再根據特殊角三角函數值得角![]() 的值;(2)根據余弦定理得bc=4,再根據三角形面積公式得結果.
的值;(2)根據余弦定理得bc=4,再根據三角形面積公式得結果.
詳解:(1)∵acosC+ccosA=-2bcosA,
由正弦定理可得:sinAcosC+sinCcosA=-2sinBcosA,
化為:sin(A+C)=sinB=2sinBcosA,sinB≠0,
可得cosA=![]() ,A∈(0,
,A∈(0,![]() ),∴A=
),∴A=![]() ;
;
(2)由![]() ,b+c=4,結合余弦定理,得a2=b2+c2-2bccosA,
,b+c=4,結合余弦定理,得a2=b2+c2-2bccosA,
∴12=(b+c)2-2bc-2bccos![]() ,即有12=16-bc,化為bc=4.
,即有12=16-bc,化為bc=4.
故△ABC的面積為S=![]() bcsinA=
bcsinA=![]() ×4×sin
×4×sin![]() =
=![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為a,E、F、G、H分別為AB、BC、CD、DA的中點.若沿EF、FG、GH、HE將四角折起,試問能折成一個四棱錐嗎?為什么?你從中能得到什么結論?對于圓錐有什么類似的結論?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正方體ABCD-A1B1C1D1的棱長為1,線段B1D1上有兩個動點E,F,且EF=![]() ,則下列結論中錯誤的是
,則下列結論中錯誤的是

A.AC⊥BE B.EF∥平面ABCD
C.三棱錐A-BEF的體積為定值 D.異面直線AE,BF所成的角為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某公園摩天輪的半徑為![]() ,圓心距地面的高度為
,圓心距地面的高度為![]() ,摩天輪做勻速轉動,每
,摩天輪做勻速轉動,每![]() 轉一圈,摩天輪上的點
轉一圈,摩天輪上的點![]() 的起始位置在最低點處.
的起始位置在最低點處.
(1)已知在時刻![]() 時
時![]() 距離地面的高度
距離地面的高度![]() ,(其中
,(其中![]() ),求
),求![]() 時
時![]() 距離地面的高度;
距離地面的高度;
(2)當離地面![]() 以上時,可以看到公園的全貌,求轉一圈中有多少時間可以看到公園的全貌?
以上時,可以看到公園的全貌,求轉一圈中有多少時間可以看到公園的全貌?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年高考特別強調了要增加對數學文化的考查,為此某校高三年級特命制了一套與數學文化有關的專題訓練卷(文、理科試卷滿分均為100分),并對整個高三年級的學生進行了測試,現從這些學生中隨機抽取了50名學生的成績,按照成績為![]() ,
,![]() ,…,
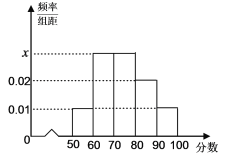
,…,![]() 分成了5組,制成了如圖所示的頻率分布直方圖(假定每名學生的成績均不低于50分).
分成了5組,制成了如圖所示的頻率分布直方圖(假定每名學生的成績均不低于50分).
(Ⅰ)求頻率分布直方圖中的![]() 的值,并估計所抽取的50名學生成績的中位數(用分數表示);
的值,并估計所抽取的50名學生成績的中位數(用分數表示);
(Ⅱ)若利用分層抽樣的方法從樣本中成績不低于70分的三組學生中抽取6人,再從這6人中隨機抽取2人參加這次考試的考后分析會,試求![]() 組中至少有1人被抽到的概率.
組中至少有1人被抽到的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com