
【題目】已知函數f(x)=aln x+![]() (a∈R).
(a∈R).
(1)當a=1時,求f(x)在x∈[1,+∞)內的最小值;
(2)若f(x)存在單調遞減區間,求a的取值范圍;
(3)求證ln(n+1)>![]() (n∈N*).
(n∈N*).
【答案】(1)最小值為f(1)=1.(2)a<![]() .(3)見解析
.(3)見解析
【解析】
試題(1)可先求f′(x),從而判斷f(x)在x∈[1,+∞)上的單調性,利用其單調性求f(x)在x∈[1,+∞)最小值;
(2)求h′(x),可得![]() ,若f(x)存在單調遞減區間,需h′(x)<0有正數解.從而轉化為:
,若f(x)存在單調遞減區間,需h′(x)<0有正數解.從而轉化為:![]() 有x>0的解.通過對a分a=0,a<0與當a>0三種情況討論解得a的取值范圍;
有x>0的解.通過對a分a=0,a<0與當a>0三種情況討論解得a的取值范圍;
(3)可用數學歸納法予以證明.當n=1時,ln(n+1)=ln2,3ln2=ln8>1![]() ,即
,即![]() 時命題成立;設當n=k時,命題成立,即
時命題成立;設當n=k時,命題成立,即![]() 成立,再去證明n=k+1時,
成立,再去證明n=k+1時,![]() 成立即可(需用好歸納假設).
成立即可(需用好歸納假設).
試題解析:(1)![]() ,定義域為
,定義域為![]() .
.
![]()
![]() 在
在![]() 上是增函數.
上是增函數.
![]() .
.
(2)因為![]()
因為若![]() 存在單調遞減區間,所以
存在單調遞減區間,所以![]() 有正數解.
有正數解.
即![]() 有
有![]() 的解
的解
當![]() 時,明顯成立 .
時,明顯成立 .
②當![]() 時,
時,![]() 開口向下的拋物線,
開口向下的拋物線,![]() 總有
總有![]() 的解;
的解;
③當![]() 時,
時,![]() 開口向上的拋物線,
開口向上的拋物線,
即方程![]() 有正根.
有正根.
因為![]() ,
,
所以方程![]() 有兩正根.
有兩正根.
當![]() 時,
時,![]() ;
;
![]() ,解得
,解得![]() .
.
綜合①②③知:![]() .
.
或:
![]() 有
有![]() 的解
的解
即![]() 有
有![]() 的解,
的解,
即![]() 有
有![]() 的解,
的解,
![]() 的最大值
的最大值![]() ,
,![]()
(3)(法一)根據(Ⅰ)的結論,當![]() 時,
時,![]() ,即
,即![]() .
.
令![]() ,則有
,則有![]() ,
,![]() .
.
![]() ,
,
![]() .
.
(法二)當![]() 時,
時,![]() .
.
![]() ,
,![]() ,即
,即![]() 時命題成立.
時命題成立.
設當![]() 時,命題成立,即
時,命題成立,即![]() .
.
![]() 時,
時,![]()
![]() .
.
根據(Ⅰ)的結論,當![]() 時,
時,![]() ,即
,即![]() .
.
令![]() ,則有
,則有![]() ,
,
則有![]() ,即
,即![]() 時命題也成立.
時命題也成立.
因此,由數學歸納法可知不等式成立.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】某公司全年的純利潤為![]() 元,其中一部分作為獎金發給
元,其中一部分作為獎金發給![]() 位職工,獎金分配方案如下首先將職工工作業績(工作業績均不相同)從大到小,由1到
位職工,獎金分配方案如下首先將職工工作業績(工作業績均不相同)從大到小,由1到![]() 排序,第1位職工得獎金
排序,第1位職工得獎金![]() 元,然后再將余額除以
元,然后再將余額除以![]() 發給第2位職工,按此方法將獎金逐一發給每位職工,并將最后剩余部分作為公司發展基金.
發給第2位職工,按此方法將獎金逐一發給每位職工,并將最后剩余部分作為公司發展基金.
(1)設![]() 為第
為第![]() 位職工所得獎金額,試求
位職工所得獎金額,試求![]() 并用
并用![]() 和
和![]() 表示
表示![]() (不必證明);
(不必證明);
(2)證明![]() 并解釋此不等式關于分配原則的實際意義;
并解釋此不等式關于分配原則的實際意義;
(3)發展基金與![]() 和
和![]() 有關,記為
有關,記為![]() 對常數
對常數![]() ,當
,當![]() 變化時,求
變化時,求![]() .(可用公式
.(可用公式![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解![]() 地區足球特色學校的發展狀況,某調查機構得到如下統計數據:
地區足球特色學校的發展狀況,某調查機構得到如下統計數據:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色學校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根據上表數據,計算![]() 與
與![]() 的相關系數
的相關系數![]() ,并說明
,并說明![]() 與
與![]() 的線性相關性強弱(已知:
的線性相關性強弱(已知:![]() ,則認為
,則認為![]() 與
與![]() 線性相關性很強;
線性相關性很強;![]() ,則認為
,則認為![]() 與
與![]() 線性相關性一般;
線性相關性一般;![]() ,則認為
,則認為![]() 與
與![]() 線性相關性較弱);
線性相關性較弱);
(Ⅱ)求![]() 關于
關于![]() 的線性回歸方程,并預測
的線性回歸方程,并預測![]() 地區2019年足球特色學校的個數(精確到個)
地區2019年足球特色學校的個數(精確到個)
參考公式: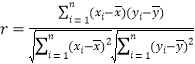 ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于集合![]() ,定義函數
,定義函數![]() 對于兩個集合
對于兩個集合![]() ,定義集合
,定義集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)寫出![]() 和
和![]() 的值,并用列舉法寫出集合
的值,并用列舉法寫出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的個數,求
所含元素的個數,求![]() 的最小值;
的最小值;
(Ⅲ)有多少個集合對![]() ,滿足
,滿足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,當P(x,y)不是原點時,定義P的“伴隨點”為![]() ;
;
當P是原點時,定義P的“伴隨點“為它自身,平面曲線C上所有點的“伴隨點”所構成的曲線![]() 定義為曲線C的“伴隨曲線”.現有下列命題:
定義為曲線C的“伴隨曲線”.現有下列命題:
①若點A的“伴隨點”是點![]() ,則點
,則點![]() 的“伴隨點”是點A
的“伴隨點”是點A
②單位圓的“伴隨曲線”是它自身;
③若曲線C關于x軸對稱,則其“伴隨曲線”![]() 關于y軸對稱;
關于y軸對稱;
④一條直線的“伴隨曲線”是一條直線.
其中的真命題是_____________(寫出所有真命題的序列).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
![]() 1
1![]() 當
當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
![]() 2
2![]() 若
若![]() 是R上的單調遞增函數,求a的取值范圍;
是R上的單調遞增函數,求a的取值范圍;
![]() 3
3![]() 若函數
若函數![]() 對任意的實數
對任意的實數![]() ,存在唯一的實數
,存在唯一的實數![]() ,使得
,使得![]() 成立,求a的值.
成立,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一次考試中,5名同學的數學、物理成績如表所示:
學生 |
|
|
|
|
|
數學 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
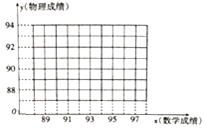
![]() 請在圖中的直角坐標系中作出這些數據的散點圖,并求出這些數據的回歸方程;
請在圖中的直角坐標系中作出這些數據的散點圖,并求出這些數據的回歸方程;
![]() 要從4名數學成績在90分以上的同學中選2名參加一項活動,以X表示選中的同學的物理成績高于90分的人數,求隨機變量X的分布列及數學期望
要從4名數學成績在90分以上的同學中選2名參加一項活動,以X表示選中的同學的物理成績高于90分的人數,求隨機變量X的分布列及數學期望![]() .
.
參考公式:線性回歸方程![]() ;,其中
;,其中![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com