
【題目】【2017黑龍江大慶實驗中學仿真模擬】如圖,在四棱錐P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD為等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q為PD的中點.
,PA⊥PD,Q為PD的中點.
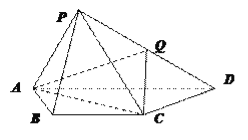
(Ⅰ)證明:CQ∥平面PAB;
(Ⅱ)求直線PD與平面AQC所成角的正弦值.
【答案】見解析
【解析】

(Ⅰ)證明 如圖所示,取PA的中點N,連接QN,
BN.在△PAD中,PN=NA,PQ=QD,
所以QN∥AD,且QN=![]() AD.
AD.
在△APD中,PA=2,PD=2![]() ,PA⊥PD,
,PA⊥PD,
所以AD=![]() =4,而BC=2,所以BC=
=4,而BC=2,所以BC=![]() AD.
AD.
又BC∥AD,所以QN∥BC,且QN=BC,
故四邊形BCQN為平行四邊形,所以BN∥CQ.
又BN平面PAB,且CQ![]() 平面PAB, 所以CQ∥平面PAB.
平面PAB, 所以CQ∥平面PAB.
(Ⅱ)如圖,取AD的中點M,連接BM;取BM的中點O,連接BO、PO.
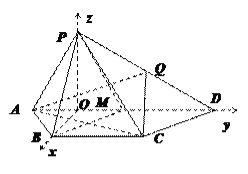
由(1)知PA=AM=PM=2,
所以△APM為等邊三角形,
所以PO⊥AM. 同理BO⊥AM.
因為平面PAD⊥平面ABCD,所以PO⊥BO.
如圖,以O為坐標原點,分別以OB,OD,OP所在直線為x軸,y軸,z軸建立空間直角坐標系,則O(0,0,0),D(0,3,0),A(0,-1,0),B(![]() ,0,0),P(0,0,
,0,0),P(0,0,![]() ),C(
),C(![]() ,2,0),
,2,0),
則![]() =(
=(![]() ,3,0).
,3,0).
因為Q為DP的中點,故Q![]() ,所以
,所以![]() =
=![]() .
.
設平面AQC的法向量為m=(x,y,z),
則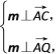 可得
可得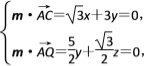
令y=-![]() ,則x=3,z=5. 故平面AQC的一個法向量為m=(3,-
,則x=3,z=5. 故平面AQC的一個法向量為m=(3,-![]() ,5).
,5).
設直線PD與平面AQC所成角為θ.
則sinθ= |cos〈![]() ,m〉|==
,m〉|==![]() .
.
從而可知直線PD與平面AQC所成角正弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若b= ![]() ,c=1,求△ABC的面積.
,c=1,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設圓弧x2+y2=1(x≥0,y≥0)與兩坐標軸正半軸圍成的扇形區域為M,過圓弧上中點A做該圓的切線與兩坐標軸正半軸圍成的三角形區域為N.現隨機在區域N內投一點B,若設點B落在區域M內的概率為P,則P的值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓C過點(1,0),且于直線x=﹣1相切.
(1)求圓心C的軌跡M的方程;
(2)A,B是M上的動點,O是坐標原點,且![]()
![]()
![]() , 求證:直線AB過定點,并求出該點坐標.
, 求證:直線AB過定點,并求出該點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017寧夏石嘴山市二模】如圖,在以![]() 為頂點的多面體中,
為頂點的多面體中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)請在圖中作出平面![]() ,使得
,使得![]() ,且
,且![]() ,并說明理由;
,并說明理由;
(2)求直線![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017福建4月質檢】如圖,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分別為棱
分別為棱![]() 的中點.
的中點.
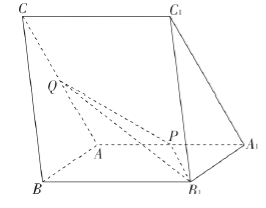
(1)在平面![]() 內過點
內過點![]() 作
作![]() 平面
平面![]() 交
交![]() 于點
于點![]() ,并寫出作圖步驟,但不要求證明.
,并寫出作圖步驟,但不要求證明.
(2)若側面![]() 側面
側面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com