
【題目】2019年春節期間,我國高速公路繼續執行“節假日高速公路免費政策”某路橋公司為掌握春節期間車輛出行的高峰情況,在某高速公路收費點記錄了大年初三上午9:20~10:40這一時間段內通過的車輛數,統計發現這一時間段內共有600輛車通過該收費點,它們通過該收費點的時刻的頻率分布直方圖如下圖所示,其中時間段9:20~9:40記作區間![]() ,9:40~10:00記作
,9:40~10:00記作![]() ,10:00~10:20記作
,10:00~10:20記作![]() ,10:20~10:40記作
,10:20~10:40記作![]() .例如:10點04分,記作時刻64.
.例如:10點04分,記作時刻64.

(1)估計這600輛車在9:20~10:40時間段內通過該收費點的時刻的平均值(同一組中的數據用該組區間的中點值代表);
(2)為了對數據進行分析,現采用分層抽樣的方法從這600輛車中抽取10輛,再從這10輛車中隨機抽取4輛,設抽到的4輛車中,在9:20~10:00之間通過的車輛數為X,求X的分布列與數學期望;
(3)由大數據分析可知,車輛在每天通過該收費點的時刻T服從正態分布![]() ,其中
,其中![]() 可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,
可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,![]() 可用樣本的方差近似代替(同一組中的數據用該組區間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(結果保留到整數).
可用樣本的方差近似代替(同一組中的數據用該組區間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(結果保留到整數).
參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
【答案】(1)10點04分(2)分布列見解析,![]() (3)819輛
(3)819輛
【解析】
(1)利用頻率分布直方圖和平均數的計算公式,即可求得這600輛車在9:20~10:40時間段內通過該收費點的時刻的平均值;
(2)結合頻率分布直方圖和分層抽樣的方法求得隨機變量![]() 的可能取值
的可能取值![]() ,求出相應的概率,得到
,求出相應的概率,得到![]() 的分布列,利用期望的公式,求得其數學期望;
的分布列,利用期望的公式,求得其數學期望;
(3)由(1)可得![]() ,得到
,得到![]() ,得到概率,即可求解在9:46~10:40這一時間段內通過的車輛數.
,得到概率,即可求解在9:46~10:40這一時間段內通過的車輛數.
(1)由題意,這600輛車在9:20~10:40時間段內通過該收費點的時刻的平均值為
![]() ,即10點04分.
,即10點04分.
(2)結合頻率分布直方圖和分層抽樣的方法可知:抽取的10輛車中,在10:00前通過的車輛數就是位于時間分組中在![]() 這一區間內的車輛數,即
這一區間內的車輛數,即![]() ,所以X的可能取值為0,1,2,3,1.
,所以X的可能取值為0,1,2,3,1.
所以![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以X的分布列為
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
所以![]() .
.
(3)由(1)可得![]() ,
,
![]() ,
,
所以![]() .
.
估計在9:46~10:40這一時間段內通過的車輛數,也就是![]() 通過的車輛數,
通過的車輛數,
由![]() ,
,
![]() ,
,
所以,估計在9:46~10:40這一時間段內通過的車輛數為![]() 輛.
輛.


科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,若存在閉區間
,若存在閉區間![]() ,使得函數
,使得函數![]() 滿足:①
滿足:①![]() 在
在![]()
上是單調函數;②![]() 在
在 ![]() 上的值域是
上的值域是![]() ,則稱區間
,則稱區間![]() 是函數
是函數 ![]() 的“和諧區間”,
的“和諧區間”,
下列結論錯誤的是( )
A.函數 ![]() 存在 “和諧區間”
存在 “和諧區間”
B.函數 ![]() 存在 “和諧區間”
存在 “和諧區間”
C.函數 ![]() 不存在 “和諧區間”
不存在 “和諧區間”
D.函數 ![]() 存在 “和諧區間”
存在 “和諧區間”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的極值;
的極值;
(2)是否存在實數![]() ,使得
,使得![]() 與
與![]() 的單調區間相同,若存在,求出
的單調區間相同,若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(3)若![]() ,求證:
,求證:![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 具備以下兩個條件:(1)至少有一條對稱軸或一個對稱中心;(2)至少有兩個零點,則稱這樣的函數為“多元素”函數,下列函數中為“多元素”函數的是_______.
具備以下兩個條件:(1)至少有一條對稱軸或一個對稱中心;(2)至少有兩個零點,則稱這樣的函數為“多元素”函數,下列函數中為“多元素”函數的是_______.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角梯形PBCD中, ![]() ,A為PD的中點,如下左圖。將
,A為PD的中點,如下左圖。將![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,點E在SD上,且
,點E在SD上,且![]() ,如下圖。
,如下圖。
(1)求證: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.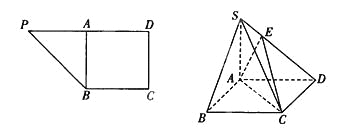
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科研團隊對某一生物生長規律進行研究,發現其生長蔓延的速度越來越快.開始在某水域投放一定面積的該生物,經過2個月其覆蓋面積為18平方米,經過3個月其覆蓋面積達到27平方米.該生物覆蓋面積![]() (單位:平方米)與經過時間
(單位:平方米)與經過時間![]() 個月的關系有兩個函數模型
個月的關系有兩個函數模型![]() 與
與![]() 可供選擇.
可供選擇.
(1)試判斷哪個函數模型更合適,并求出該模型的函數解析式;
(2)問約經過幾個月,該水域中此生物的面積是當初投放的1000倍![]() (參考數據:
(參考數據:![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com