
【題目】已知函數(shù)![]() ,其中
,其中![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(Ⅰ)當![]() ,
,![]() 時,證明:
時,證明:![]() ;
;
(Ⅱ)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的極值點的個數(shù).
的極值點的個數(shù).
【答案】(Ⅰ)見解析;(Ⅱ)見解析
【解析】試題分析:(Ⅰ)依題意![]() ,只要證
,只要證![]() ,記
,記![]() ,求得
,求得![]() ,分
,分![]() 和
和![]() 討論即可得到函數(shù)的單調性,進而得到結論;
討論即可得到函數(shù)的單調性,進而得到結論;
(Ⅱ)由![]()
![]() ,記
,記![]() ,
,![]() ,(1)當
,(1)當![]() 時,得到
時,得到![]() 存在唯一
存在唯一![]() ,且當
,且當![]() 時,
時,![]() ;當
;當![]() ,
,![]() ,再分
,再分![]() 和
和![]() 和
和![]() 三種情形討論,得到地產(chǎn)是
三種情形討論,得到地產(chǎn)是![]() 有一個極大值點
有一個極大值點![]() 和一個極小值點
和一個極小值點![]() ,(2)當
,(2)當![]() 時,顯然
時,顯然![]() 在
在![]() 單調遞減;在
單調遞減;在![]() 上單調遞增,綜上所述即可得到結論.
上單調遞增,綜上所述即可得到結論.
試題解析:
(Ⅰ)依題意![]() ,因為
,因為![]() ,只要證
,只要證![]() ,
,
記![]() ,
,![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
所以![]() ,即
,即![]() ,原不等式成立.
,原不等式成立.
(Ⅱ)![]()
![]()
![]()
![]() ,
,
記![]() ,
,![]() .
.
(1)當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,
,![]() ,
,
所以存在唯一![]() ,
,![]() ,且當
,且當![]() 時,
時,![]() ;當
;當![]() ,
,![]() ,
,
①若![]() ,即
,即![]() 時,對任意
時,對任意![]() ,
,![]() ,此時
,此時![]() 在
在![]() 上單調遞增,無極值點.
上單調遞增,無極值點.
②若![]() ,即
,即![]() 時,此時當
時,此時當![]() 或
或![]() 時,
時,![]() .即
.即![]() 在
在![]() ,
,![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞減.
上單調遞減.
此時![]() 有一個極大值點
有一個極大值點![]() 和一個極小值點-1.
和一個極小值點-1.
③若![]() ,即
,即![]() 時,此時當
時,此時當![]() 或
或![]() 時,
時,![]() .即
.即![]() 在
在![]() ,
,![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞減.
上單調遞減.
此時![]() 有一個極大值點-1和一個極小值點
有一個極大值點-1和一個極小值點![]() .
.
(2)當![]() 時,
時,![]() ,所以
,所以![]() ,顯然
,顯然![]() 在
在![]() 單調遞減;在
單調遞減;在![]() 上單調遞增.
上單調遞增.
綜上可得:①當![]() 或
或![]() 時,
時,![]() 有兩個極值點;
有兩個極值點;
②當![]() 時,
時,![]() 無極值點;
無極值點;
③當![]() 時,
時,![]() 有一個極值點.
有一個極值點.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:高中數(shù)學 來源: 題型:
【題目】在四棱錐![]() 中,底面
中,底面![]() 是正方形,頂點
是正方形,頂點![]() 在底面的射影是底面的中心,且各頂點都在同一球面上,若該四棱錐的側棱長為
在底面的射影是底面的中心,且各頂點都在同一球面上,若該四棱錐的側棱長為![]() ,體積為4,且四棱錐的高為整數(shù),則此球的半徑等于( )(參考公式:
,體積為4,且四棱錐的高為整數(shù),則此球的半徑等于( )(參考公式:![]() )
)
A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“中國式過馬路”存在很大的交通安全隱患.某調查機構為了解路人對“中國式過馬路”的態(tài)度是否與性別有關,從馬路旁隨機抽取30名路人進行了問卷調查,得到了如下列聯(lián)表:
項目 | 男性 | 女性 | 總計 |
反感 | 10 | ||
不反感 | 8 | ||
總計 | 30 |
已知在這30人中隨機抽取1人抽到反感“中國式過馬路”的路人的概率是![]() .
.
(1)請將上面的列聯(lián)表補充完整(直接寫結果,不需要寫求解過程),并據(jù)此資料分析反感“中國式過馬路”與性別是否有關?
(2)若從這30人中的女性路人中隨機抽取2人參加一活動,記反感“中國式過馬路”的人數(shù)為X,求X的分布列和數(shù)學期望.
附:K2=![]()
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年,國家逐步推行全新的高考制度.新高考不再分文理科,某省采用3+3模式,其中語文、數(shù)學、外語三科為必考科目,滿分各150分,另外考生還要依據(jù)想考取的高校及專業(yè)的要求,結合自己的興趣愛好等因素,在思想政治、歷史、地理、物理、化學、生物6門科目中自選3門參加考試(6選3),每科目滿分100分.為了應對新高考,某高中從高一年級1000名學生(其中男生550人,女生450人)中,采用分層抽樣的方法從中抽取![]() 名學生進行調查.
名學生進行調查.
(1)已知抽取的![]() 名學生中含男生55人,求
名學生中含男生55人,求![]() 的值;
的值;
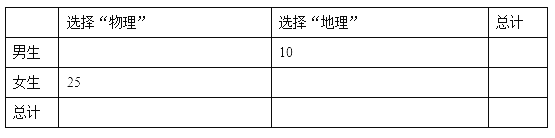
(2)學校計劃在高一上學期開設選修中的“物理”和“地理”兩個科目,為了了解學生對這兩個科目的選課情況,對在(1)的條件下抽取到的![]() 名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目且只能選擇一個科目),下表是根據(jù)調查結果得到的
名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目且只能選擇一個科目),下表是根據(jù)調查結果得到的![]() 列聯(lián)表. 請將列聯(lián)表補充完整,并判斷是否有 99%的把握認為選擇科目與性別有關?說明你的理由;
列聯(lián)表. 請將列聯(lián)表補充完整,并判斷是否有 99%的把握認為選擇科目與性別有關?說明你的理由;
(3)在抽取到的女生中按(2)中的選課情況進行分層抽樣,從中抽出9名女生,再從這9名女生中抽取4人,設這4人中選擇“地理”的人數(shù)為![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
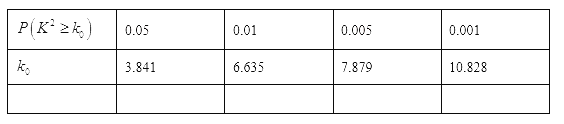
附:![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)f(x)=|x﹣a|+|x![]() |(a>0).
|(a>0).
(1)若不等式f(x)﹣| x![]() |≥4x的解集為{x|x≤1},求實數(shù)a的值;
|≥4x的解集為{x|x≤1},求實數(shù)a的值;
(2)證明:f(x)![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如果函數(shù)![]() 在定義域內存在區(qū)間[a,b],使
在定義域內存在區(qū)間[a,b],使![]() 在[a,b]上的值域是[2a,2b],那么稱
在[a,b]上的值域是[2a,2b],那么稱![]() 為“倍增函數(shù)”。
為“倍增函數(shù)”。
(I)判斷![]() =
=![]() 是否為“倍增函數(shù)”,并說明理由;
是否為“倍增函數(shù)”,并說明理由;
(II)證明:函數(shù)![]() =
=![]() 是“倍增函數(shù)”;
是“倍增函數(shù)”;
(III)若函數(shù)![]() =ln(
=ln(![]() )是“倍增函數(shù)”,寫出實數(shù)m的取值范圍。(只需寫出結論)
)是“倍增函數(shù)”,寫出實數(shù)m的取值范圍。(只需寫出結論)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓具有如下性質:若![]() 、
、![]() 是橢圓
是橢圓![]() 上關于原點對稱的兩個點,點
上關于原點對稱的兩個點,點![]() 是橢圓上的任意一點,當直線
是橢圓上的任意一點,當直線![]() 、
、![]() 的斜率都存在,并記為
的斜率都存在,并記為![]() 、
、![]() 時,則
時,則![]() 與
與![]() 之積是與點
之積是與點![]() 位置無關的定值.試寫出雙曲線
位置無關的定值.試寫出雙曲線![]() 具有的類似的性質,并加以證明.
具有的類似的性質,并加以證明.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com