
(本小題滿分12分)設(shè)函數(shù)f(x)=m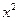 -mx-1.
-mx-1.
(1)若對于一切實數(shù)x,f(x)<0恒成立,求m的取值范圍;
(2)對于x∈[1,3],f(x)<0恒成立,求m的取值范圍.
科目:高中數(shù)學(xué) 來源: 題型:解答題
f (x)是偶函數(shù),且在(0,+∞)上是增函數(shù),若x∈[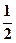 ,1]時,不等式f (ax+1)≤f (x-2)恒成立,則求實數(shù)a的取值范圍?
,1]時,不等式f (ax+1)≤f (x-2)恒成立,則求實數(shù)a的取值范圍?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分14分)
已知函數(shù)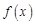 和
和 的圖象關(guān)于原
的圖象關(guān)于原 點對稱,且
點對稱,且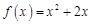 .
.
(Ⅰ)求函數(shù) 的解析式;
的解析式;
(Ⅱ)解不等式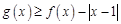 ;
;
(Ⅲ)若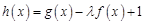 在
在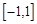 上是增函數(shù),求實數(shù)
上是增函數(shù),求實數(shù)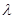 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè) ,
,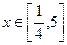 , 其中
, 其中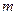 是不等于零的常數(shù),
是不等于零的常數(shù),
(1)、(理)寫出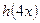 的定義域(2分);
的定義域(2分);
(文)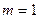 時,直接寫出
時,直接寫出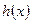 的值域(4分)
的值域(4分)
(2)、(文、理)求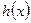 的單調(diào)遞增區(qū)間(理5分,文8分);
的單調(diào)遞增區(qū)間(理5分,文8分);
(3)、已知函數(shù)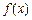
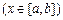 ,定義:
,定義: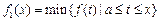
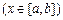 ,
,
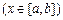 .其中,
.其中, 表示函數(shù)
表示函數(shù)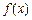 在
在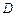 上的最小值,
上的最小值,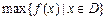 表示函數(shù)
表示函數(shù)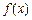 在
在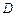
 上的最大值.例如:
上的最大值.例如: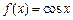 ,
,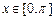 ,則
,則 ,
,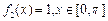 ,
,
(理)當(dāng)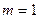 時,設(shè)
時,設(shè)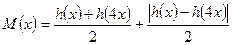 ,不等式
,不等式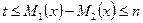
恒成立,求 的取值范圍(11分);
的取值范圍(11分);
(文)當(dāng)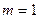 時,
時,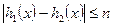 恒成立,求
恒成立,求 的取值范圍(8分);
的取值范圍(8分);
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
隨著機構(gòu)改革工作的深入進行,各單位要減員增效,有一家公司現(xiàn)有職員2a人(140<2a<420,且a為偶數(shù) ,每人每年可創(chuàng)利10萬元.據(jù)評估,在經(jīng)營條件不變的前提下,若裁員x人,則留崗職員每人每年多創(chuàng)利0.1x萬元,但公司需付下崗職員每人每年4萬元的生活費,并且該公司正常運轉(zhuǎn)情況下,所裁人數(shù)不超過50人,為獲得最大的經(jīng)濟效益,該公司應(yīng)裁員多少人?
,每人每年可創(chuàng)利10萬元.據(jù)評估,在經(jīng)營條件不變的前提下,若裁員x人,則留崗職員每人每年多創(chuàng)利0.1x萬元,但公司需付下崗職員每人每年4萬元的生活費,并且該公司正常運轉(zhuǎn)情況下,所裁人數(shù)不超過50人,為獲得最大的經(jīng)濟效益,該公司應(yīng)裁員多少人?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知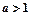 ,函數(shù)
,函數(shù)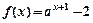
(1)求 的反函數(shù)
的反函數(shù)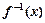 ;
;
(2)若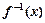 在[0,1]上的最大值與最小值互為相反數(shù),求
在[0,1]上的最大值與最小值互為相反數(shù),求 ;
;
(3)若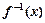 的圖像不經(jīng)過第二象限,求
的圖像不經(jīng)過第二象限,求 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知函數(shù)
 ,其圖象過點(
,其圖象過點( ,
, ).
).
(1)求 的值及
的值及 最小正周期;
最小正周期;
(2)將函數(shù) 的圖象上各點的橫坐標縮短到原來的
的圖象上各點的橫坐標縮短到原來的 ,縱坐標不變,得到函數(shù)
,縱坐標不變,得到函數(shù)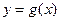 的圖象,求函數(shù)
的圖象,求函數(shù) 在[0,
在[0,  ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com