【題目】某公司為了準確地把握市場，做好產品生產計劃，對過去四年的數據進行整理得到了第
年與年銷量
(單位：萬件)之間的關系如表：
(Ⅰ)在圖中畫出表中數據的散點圖；
(Ⅱ)根據(Ⅰ)中的散點圖擬合
與
的回歸模型，并用相關系數甲乙說明；
(Ⅲ)建立
關于
的回歸方程，預測第5年的銷售量約為多少？.
附注：參考數據：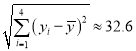 
， 
， 
.
參考公式：相關系數
，
回歸方程
中斜率和截距的最小二乘法估計公式分別為：
， 
.
【答案】(Ⅰ)散點圖見解析；(Ⅱ)答案見解析；(Ⅲ) 71萬件.
【解析】試題分析：
(Ⅰ) 根據所給數據易得散點圖;
(Ⅱ) 利用所提供的數據與公式求出
與
的相關系數r,即可得出結論;
(Ⅲ) 由題中所提供的數據,分別求出
的值,則可得回歸直線方程,再將
代入回歸直線方程可得結論.
試題解析：
(Ⅰ)作出散點圖如圖：
(Ⅱ)由(Ⅰ)散點圖可知，各點大致分布在一條直線附近，由題中所給表格及參考數據得：
， 
， 
， 
， 
， 
， 
，
.
∵
與
的相關系數近似為0.9996，說明
與
的線性相關程度相當大，
∴可以用線性回歸模型擬合
與
的關系.
(Ⅲ)由(Ⅱ)知： 
， 
， 
， 
， 
，
， 
，
故
關于
的回歸直線方程為
，
當
時， 
，
所以第5年的銷售量約為71萬件.
科目：高中數學 來源： 題型：
【題目】數列{an}滿足a1=1， 
（n∈N+）．
（1）證明：數列 
是等差數列；
（2）求數列{an}的通項公式an；
（3）設bn=n（n+1）an ， 求數列{bn}的前n項和Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（13分）如圖，橢圓
經過點
，離心率
，直線l的方程為
．
（1）求橢圓C的方程；
（2）
是經過右焦點
的任一弦（不經過點
），設直線與直線
相交于點
，記
、
、
的斜率分別為
、
、
．問：是否存在常數
，使得
? 若存在，求的值； 若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某經銷商從外地水產養殖廠購進一批小龍蝦，并隨機抽取40只進行統計，按重量分類統計結果如下圖：
（1）記事件
為：“從這批小龍蝦中任取一只，重量不超過35
的小龍蝦”，求
的估計值；
（2）若購進這批小龍蝦100千克，試估計這批小龍蝦的數量；
（3）為適應市場需求，了解這批小龍蝦的口感，該經銷商將這40只小龍蝦分成三個等級，如下表：
等級 | 一等品 | 二等品 | 三等品 |
重量（ |
|
|
|
按分層抽樣抽取10只，再隨機抽取3只品嘗，記
為抽到二等品的數量，求抽到二級品的期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數y=f（x），若在其定義域內存在x0 ， 使得x0f（x0）=1成立，則稱x0為函數f（x）的“反比點”．下列函數中具有“反比點”的是
①f（x）=﹣2x+2
； ②f（x）=sinx，x∈[0，2π]；
③f（x）=x+
， x∈（0，+∞）；④f（x）=ex； ⑤f（x）=﹣2lnx．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場擬對某商品進行促銷，現有兩種方案供選擇，每種促銷方案都需分兩個月實施，且每種方案中第一個月與第二個月的銷售相互獨立.根據以往促銷的統計數據，若實施方案1，預計第一個月的銷量是促銷前的1.2倍和1.5倍的概率分別是0.6和0.4，第二個月的銷量是第一個月的1.4倍和1.6倍的概率都是0.5；若實施方案2，預計第一個月的銷量是促銷前的1.4倍和1.5倍的概率分別是0.7和0.3，第二個月的銷量是第一個月的1.2倍和1.6倍的概率分別是0.6和0.4.令
表示實施方案
的第二個月的銷量是促銷前銷量的倍數.
（Ⅰ）求
， 
的分布列；
（Ⅱ）不管實施哪種方案， 
與第二個月的利潤之間的關系如下表，試比較哪種方案第二個月的利潤更大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某省高考改革新方案，不分文理科，高考成績實行“
”的構成模式，第一個“3”是語文、數學、外語，每門滿分150分，第二個“3”由考生在思想政治、歷史、地理、物理、化學、生物6個科目中自主選擇其中3個科目參加等級性考試，每門滿分100分，高考錄取成績卷面總分滿分750分.為了調查學生對物理、化學、生物的選考情況，將“某市某一屆學生在物理、化學、生物三個科目中至少選考一科的學生”記作學生群體
，從學生群體
中隨機抽取了50名學生進行調查，他們選考物理，化學，生物的科目數及人數統計如下表：
(I)從所調查的50名學生中任選2名，求他們選考物理、化學、生物科目數量不相等的概率；
(II)從所調查的50名學生中任選2名，記
表示這2名學生選考物理、化學、生物的科目數量之差的絕對值，求隨機變量
的分布列和數學期望；
(III)將頻率視為概率，現從學生群體
中隨機抽取4名學生，記其中恰好選考物理、化學、生物中的兩科目的學生數記作
，求事件“
”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
