【題目】已知函數
.
（1）討論
的單調性；
（2）討論在
上的零點個數.
【答案】（1）當
時，
在
上單調遞減，當
時，在
上單調遞增，在
上單調遞減；（2）當
時，在
上沒有零點，當
時，在上只有一個零點，當
時，在上有兩個零點.
【解析】
（1）利用函數的導函數，分類討論參數
，得出的單調性；
（2）轉化問題，原函數有零點即函數
有解，求導得出的單調性和極值，分類討論得出在上的零點個數.
解：（1）∵
，
∴
，
當時，
恒成立，
∴在上單調遞減，
當
時，
令
，得
，令，得
.
∴在上單調遞增，在上單調遞減，
綜上所述，當時，在上單調遞減，
當時，在上單調遞增，在上單調遞減；
（2）令
，得
，
設，則
.
令
，得
，
令
，得
，
∴
在
上單調遞減，在
上單調遞增，則
.
當
時，
在上無解，所以在上沒有零點；
當時，在上有且僅一個解，所以在上有一個零點；
當時，在上有兩個解，所以在上有兩個零點.
綜上，當時，在上沒有零點；
當時，在上只有一個零點；
當時，在上有兩個零點.
仁愛英語同步練習冊系列答案
學習實踐園地系列答案科目：高中數學 來源： 題型：
【題目】已知向量
＝(cosx，sinx)，
＝(cosx，﹣sinx)，函數
．
（1）若
，x
(0，
)，求tan(x＋
)的值；
（2）若
，
(
，
)，
，
(0，)，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
時代悄然來臨，為了研究中國手機市場現狀，中國信通院統計了2019年手機市場每月出貨量以及與2018年當月同比增長的情況，得到如下統計圖，根據該統計圖，下列說法錯誤的是（ ）
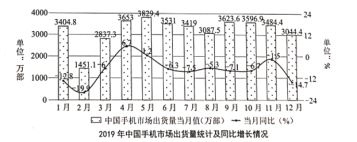
A.2019年全年手機市場出貨量中，5月份出貨量最多
B.2019年下半年手機市場各月份出貨量相對于上半年各月份波動小
C.2019年全年手機市場總出貨量低于2018年全年總出貨量
D.2018年12月的手機出貨量低于當年8月手機出貨量
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）為奇函數，且當x≥0時，f（x）＝ex﹣cosx，則不等式f（2x﹣1）+f（x﹣2）＞0的解集為( )
A.（﹣∞，1）B.（﹣∞，
）C.（，+∞）D.（1，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場推出消費抽現金活動，顧客消費滿1000元可以參與一次抽獎，該活動設置了一等獎、二等獎、三等獎以及參與獎，獎金分別為：一等獎200元、二等獎100元、三等獎50元、參與獎20元，具體獲獎人數比例分配如圖，則下列說法中錯誤的是（ ）
A.獲得參與獎的人數最多
B.各個獎項中一等獎的總金額最高
C.二等獎獲獎人數是一等獎獲獎人數的兩倍
D.獎金平均數為
元
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學有教師400人，其中高中教師240人．為了了解該校教師每天課外鍛煉時間，現利用分層抽樣的方法從該校教師中隨機抽取了100名教師進行調查，統計其每天課外鍛煉時間（所有教師每天課外鍛煉時間均在
分鐘內），將統計數據按
，
，
，…，
分成6組，制成頻率分布直方圖如下：假設每位教師每天課外鍛煉時間相互獨立，并稱每天鍛煉時間小于20分鐘為缺乏鍛煉．
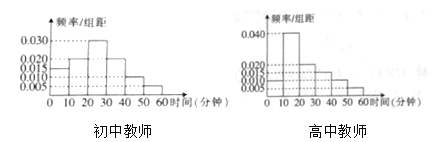
（1）試估計本校教師中缺乏鍛煉的人數；
（2）從全市高中教師中隨機抽取3人，若
表示每天課外鍛煉時間少于10分鐘的人數，以這60名高中教師每天課外鍛煉時間的頻率代替每名高中教師每天課外鍛煉時間發生的概率，求隨機變量的分布列與數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
