
【題目】在研究塞卡病毒(Zika virus)某種疫苗的過程中,為了研究小白鼠連續接種該種疫苗后出現![]() 癥狀的情況,做接種試驗,試驗設計每天接種一次,連續接種3天為一個接種周期.已知小白鼠接種后當天出現
癥狀的情況,做接種試驗,試驗設計每天接種一次,連續接種3天為一個接種周期.已知小白鼠接種后當天出現![]() 癥狀的概率為
癥狀的概率為![]() ,假設每次接種后當天是否出現
,假設每次接種后當天是否出現![]() 癥狀與上次接種無關.
癥狀與上次接種無關.
(1)若出現![]() 癥狀即停止試驗,求試驗至多持續一個接種周期的概率;
癥狀即停止試驗,求試驗至多持續一個接種周期的概率;
(2)若在一個接種周期內出現3次![]() 癥狀,則這個接種周期結束后終止試驗,試驗至多持續3個周期,設接種試驗持續的接種周期數為
癥狀,則這個接種周期結束后終止試驗,試驗至多持續3個周期,設接種試驗持續的接種周期數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知定義在區間[﹣ ![]() ,π]上的函數y=f(x)的圖象關于直線x=
,π]上的函數y=f(x)的圖象關于直線x= ![]() 對稱,當x≥
對稱,當x≥ ![]() 時,函數y=sinx.
時,函數y=sinx.
(1)求f(﹣ ![]() ),f(﹣
),f(﹣ ![]() )的值;
)的值;
(2)求y=f(x)的表達式
(3)若關于x的方程f(x)=a有解,那么將方程在a取某一確定值時所求得的所有解的和記為Ma , 求Ma的所有可能取值及相應a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
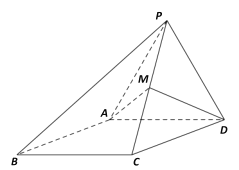
【題目】如圖,四棱錐![]() ,側面
,側面![]() 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面![]() 是
是![]() 的菱形,
的菱形, ![]() 為棱
為棱![]() 上的動點,且
上的動點,且![]() .
.
(I)求證: ![]() 為直角三角形;
為直角三角形;
(II)試確定![]() 的值,使得二面角
的值,使得二面角![]() 的平面角余弦值為
的平面角余弦值為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2mx+m2+4m﹣2.
(1)若函數f(x)在區間[0,1]上是單調遞減函數,求實數m的取值范圍;
(2)若函數f(x)在區間[0,1]上有最小值﹣3,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某紡紗廠生產甲、乙兩種棉紗,已知生產甲種棉紗1噸需耗一級籽棉2噸、二級籽棉1噸;生產乙種棉紗1噸需耗一級籽棉1噸,二級籽棉2噸.每1噸甲種棉紗的利潤為900元,每1噸乙種棉紗的利潤為600元.工廠在生產這兩種棉紗的計劃中,要求消耗一級籽棉不超過250噸,二級籽棉不超過300噸.問甲、乙兩種棉紗應各生產多少噸,能使利潤總額最大?并求出利潤總額的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 (本小題滿分12分)
如圖, 在四面體ABOC中, ![]() , 且
, 且![]() .
.
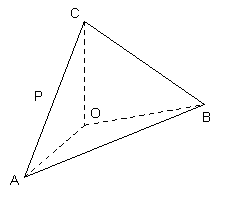
(Ⅰ)設為![]() 為
為![]() 的中點, 證明: 在
的中點, 證明: 在![]() 上存在一點
上存在一點![]() ,使
,使![]() ,并計算
,并計算![]() ;
;
(Ⅱ)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4![]() 4:坐標系與參數方程
4:坐標系與參數方程
在平面直角坐標系![]() 中,圓C的參數方程為
中,圓C的參數方程為 ,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線
,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,A,B兩點的極坐標分別為
,A,B兩點的極坐標分別為![]() .
.
(Ⅰ)求圓C的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)點P是圓C上任一點,求△PAB面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com