
【題目】已知函數f(x)=ax+ln x,其中a為常數.
(1)當a=-1時,求f(x)的單調遞增區間.
(2)當0<-![]() <e時,若f(x)在區間(0,e)上的最大值為-3,求a的值.
<e時,若f(x)在區間(0,e)上的最大值為-3,求a的值.
(3)當a=-1時,試推斷方程|f(x)|=![]() 是否有實數根.
是否有實數根.
【答案】(1)(0,1).(2) ![]() .(3)方程沒有實數根.
.(3)方程沒有實數根.
【解析】試題分析:(1)先求函數導數,再求導函數零點,列表分析可得導函數符號,即得f(x)的單調遞增區間.(2)先求函數導數,再求導函數零點,列表分析可得導函數符號,即得f(x)的單調性,最后根據單調性確定函數最大值,由最大值為-3解方程可得a的值.(3)先根據(1)得|f(x)|最小值為1,再利用導數研究![]() 單調性并確定最大值,且小于1,因此兩函數無交點
單調性并確定最大值,且小于1,因此兩函數無交點
試題解析:(1)由已知可知函數f(x)的定義域為{x|x>0},
當a=-1時,f(x)=-x+ln x(x>0),f′(x)=![]() (x>0);
(x>0);
當0<x<1時,f′(x)>0;當x>1時,f′(x)<0.
所以f(x)的單調遞增區間為(0,1).
(2)因為f′(x)=a+![]() (x>0),令f′(x)=0,解得x=-
(x>0),令f′(x)=0,解得x=-![]() ;
;
由f′(x)>0,解得0<x<-![]() ;由f′(x)<0,解得-
;由f′(x)<0,解得-![]() <x<e.
<x<e.
從而f(x)的單調遞增區間為![]() ,遞減區間為
,遞減區間為![]() ,
,
所以,f(x)max=f![]() =-1+ln
=-1+ln![]() =-3.
=-3.
解得a=-e2.
(3)由(1)知當a=-1時,f(x)max=f(1)=-1,
所以|f(x)|≥1.
令g(x)=![]() +
+![]() ,則g′(x)=
,則g′(x)=![]() .
.
當0<x<e時,g′(x)>0;
當x>e時,g′(x)<0.
從而g(x)在(0,e)上單調遞增,在(e,+∞)上單調遞減.
所以g(x)max=g(e)=![]() +
+![]() <1,
<1,
所以,|f(x)|>g(x),即|f(x)|>![]() +
+![]() ,
,
所以,方程|f(x)|=![]() +
+![]() 沒有實數根.
沒有實數根.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源: 題型:
【題目】一個化肥廠生產甲、乙兩種混合肥料,生產1車皮甲種肥料的主要原料是磷酸鹽4噸,硝酸鹽18噸;生產1車皮乙種肥料需要的主要原料是磷酸鹽1噸,硝酸鹽15噸.現庫存磷酸鹽10噸,硝酸鹽66噸,在此基礎上生產這兩種混合肥料.如果生產1車皮甲種肥料產生的利潤為12 000元,生產1車皮乙種肥料產生的利潤為7 000元,那么可產生的最大利潤是( )
A. 29 000元 B. 31 000元 C. 38 000元 D. 45 000元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,點
兩點,點![]() 為
為![]() 的中點,點
的中點,點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1 ,在△ABC中,AB=BC=2, ∠B=90°,D為BC邊上一點,以邊AC為對角線做平行四邊形ADCE,沿AC將△ACE折起,使得平面ACE ⊥平面ABC,如圖2.
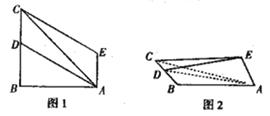
(1)在圖 2中,設M為AC的中點,求證:BM丄AE;
(2)在圖2中,當DE最小時,求二面角A -DE-C的平面角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】園林管理處擬在公園某區域規劃建設一半徑為![]() 米圓心角為
米圓心角為![]() (弧度)的扇形景觀水池,其中
(弧度)的扇形景觀水池,其中![]() 為扇形
為扇形![]() 的圓心,同時緊貼水池周邊建一圈理想的無寬度步道,要求總預算費用不超過
的圓心,同時緊貼水池周邊建一圈理想的無寬度步道,要求總預算費用不超過![]() 萬元,水池造價為每平方米
萬元,水池造價為每平方米![]() 元,步道造價為每米
元,步道造價為每米![]() 元.
元.
(1)當![]() 和
和![]() 分別為多少時,可使廣場面積最大,并求出最大值;
分別為多少時,可使廣場面積最大,并求出最大值;
(2)若要求步道長為![]() 米,則可設計出水池最大面積是多少.
米,則可設計出水池最大面積是多少.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(-2,0),B(2,0),曲線C上的動點P滿足![]() .
.
(1)求曲線C的方程;
(2)若過定點M(0,-2)的直線l與曲線C有公共點,求直線l的斜率k的取值范圍;
(3)若動點Q(x,y)在曲線C上,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,A、B、C的對邊分別為a,b,c,已知向量![]() ,n=(c,b-2a),且m·n=0.
,n=(c,b-2a),且m·n=0.
(1)求角C的大小;
(2)若點D為邊AB上一點,且滿足![]() ,
, ![]() ,
, ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系的原點為極點,x軸正半軸為極軸建立極坐標系.已知圓C的極坐標方程為ρ=2sin θ,直線l的參數方程為![]() (t為參數),若l與C交于A,B兩點.
(t為參數),若l與C交于A,B兩點.
(Ⅰ)求|AB|;
(Ⅱ)設P(1,2),求|PA|·|PB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com