
【題目】已知函數(shù)f(x)=x﹣ ![]() 存在單調(diào)遞減區(qū)間,且y=f(x)的圖象在x=0處的切線l與曲線y=ex相切,符合情況的切線l( )
存在單調(diào)遞減區(qū)間,且y=f(x)的圖象在x=0處的切線l與曲線y=ex相切,符合情況的切線l( )
A.有3條
B.有2條
C.有1條
D.不存在
【答案】D
【解析】解:函數(shù)f(x)=x﹣ ![]() 的導(dǎo)數(shù)為f′(x)=1﹣
的導(dǎo)數(shù)為f′(x)=1﹣ ![]()
![]() ,
,
依題意可知,f′(x)<0在(﹣∞,+∞)有解,
①a<0時,f′(x)<0 在(﹣∞,+∞)無解,不符合題意;
②a>0時,f′(x)>0即a> ![]() ,lna>
,lna> ![]() ,x<alna符合題意,則a>0.
,x<alna符合題意,則a>0.
易知,曲線y=f(x)在x=0處的切線l的方程為y=(1﹣ ![]() )x﹣1.
)x﹣1.
假設(shè)l與曲線y=ex相切,設(shè)切點為(x0 , y0),
即有 ![]() =1﹣
=1﹣ ![]() =(1﹣
=(1﹣ ![]() )x0﹣1,
)x0﹣1,
消去a得 ![]() ,設(shè)h(x)=exx﹣ex﹣1,
,設(shè)h(x)=exx﹣ex﹣1,
則h′(x)=exx,令h′(x)>0,則x>0,
所以h(x)在(﹣∞,0)上單調(diào)遞減,在(0,+∞)上單調(diào)遞增,
當x→﹣∞,h(x)→﹣1,x→+∞,h(x)→+∞,
所以h(x)在(0,+∞)有唯一解,則 ![]() ,
,
而a>0時, ![]() ,與
,與 ![]() 矛盾,所以不存在.
矛盾,所以不存在.
故選:D.


 計算高手系列答案
計算高手系列答案科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)y=4x3+ax2+bx+5在x= ![]() 與x=﹣1時有極值.
與x=﹣1時有極值.
(1)寫出函數(shù)的解析式;
(2)指出函數(shù)的單調(diào)區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的導(dǎo)函數(shù).
(1)若f(x)≥ag(x)恒成立,求實數(shù)a的取值范圍;
(2)設(shè)n∈N* , 證明: ![]() +
+ ![]() +…+
+…+ ![]() <ln(n+1).
<ln(n+1).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓Γ: ![]() +
+ ![]() =1(a>b>0)的右焦點與短軸兩端點構(gòu)成一個面積為2的等腰直角三角形,O為坐標原點:
=1(a>b>0)的右焦點與短軸兩端點構(gòu)成一個面積為2的等腰直角三角形,O為坐標原點: 
(1)求橢圓Г的方程:
(2)設(shè)點A在橢圓Г上,點B在直線y=2上,且OA⊥OB,求證: ![]() +
+ ![]() 為定值:
為定值:
(3)設(shè)點C在Γ上運動,OC⊥OD,且點O到直線CD距離為常數(shù)d(0<d<2),求動點D的軌跡方程:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】從某學校高三年級共800名男生中隨機抽取50人測量身高.數(shù)據(jù)表明,被測學生身高全部介于155cm到195cm之間,將測量結(jié)果按如下方式分成八組:第一組[155,160);第二組[160,165);…;第八組[190,195].如圖是按上述分組方法得到的頻率分布直方圖的一部分.已知第一組與第八組人數(shù)相同,第六組比第七組少1人. 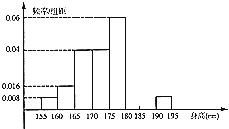
(1)估計這所學校高三年級全體男生身高在180cm以上(含180cm)的人數(shù);
(2)若從身高屬于第六組和第八組的所有男生中隨機抽取兩人,記他們的身高分別為x,y,求滿足“|x﹣y|≤5”的事件的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是平行四邊形,∠BCD=135°,側(cè)面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F(xiàn)分別為BC,AD的中點,點M在線段PD上. 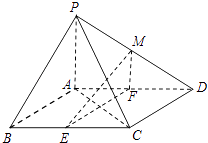
(1)求證:EF⊥平面PAC;
(2)如果直線ME與平面PBC所成的角和直線ME與平面ABCD所成的角相等,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【2017河北唐山三模】已知函數(shù)![]() ,
, ![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 有唯一零點
有唯一零點![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為矩形,PA⊥平面ABCD,AB=PA=1,AD= ![]() ,F(xiàn)是PB中點,E為BC上一點.
,F(xiàn)是PB中點,E為BC上一點. 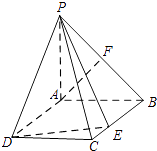
(1)求證:AF⊥平面PBC;
(2)當BE為何值時,二面角C﹣PE﹣D為45°.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=120°,AC=3,△ABC的面積等于 ![]() ,D為邊長BC上一點.
,D為邊長BC上一點. 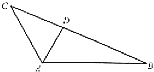
(1)求BC的長;
(2)當AD= ![]() 時,求cos∠CAD的值.
時,求cos∠CAD的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com