
【題目】函數![]()
(1)討論函數![]() 的單凋性;
的單凋性;
(2)若存在![]() 使得對任意的
使得對任意的![]() 不等式
不等式![]() (其中e為自然對數的底數)都成立,求實數
(其中e為自然對數的底數)都成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)略;(Ⅱ)![]() .
.
【解析】
試題分析:(Ⅰ)求導,討論參數的取值確定導函數的正負,進而判定函數的單調性;(Ⅱ)先借助(Ⅰ)的結論求出不等式左邊的最小值,即將存在性問題轉化為左邊的最小值大于不等式右邊,再作差構造函數,將不等式恒成立問題轉化為求函數的最值問題.
試題解析:(I)![]()
![]() ,記
,記![]()
(i)當![]() 時,因為
時,因為![]() ,所以
,所以![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
(ii)當![]() 時,因為
時,因為![]() ,
,
所以![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
(iii)當![]() 時,由
時,由![]() ,解得
,解得![]() ,
,
所以函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
在區間![]() 上單調遞增
上單調遞增
(II)由(I)知當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
所以當![]() 時,函數
時,函數![]() 的最大值是
的最大值是![]() ,對任意的
,對任意的![]() ,
,
都存在![]() ,使得不等式
,使得不等式![]() 成立,
成立,
等價于對任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
即對任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
記![]() ,由
,由![]() ,
,
![]() ,
,
由![]() 得
得![]() 或
或![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
①當![]() 時,
時,![]() ,且
,且![]() 時,
時,![]() ,
,
![]() 時,
時,![]() ,所以
,所以![]() ,
,
所以![]() 時,
時,![]() 恒成立;
恒成立;
②當![]() 時,
時,![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
此時![]() 單調遞增,且
單調遞增,且![]() ,
,
所以![]() 時,
時,![]() 成立;
成立;
③當![]() 時,
時,![]() ,
,![]() ,
,
所以存在![]() 使得
使得![]() ,因此
,因此![]() 不恒成立.
不恒成立.
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.
另解(II)由(Ⅰ)知,當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
所以![]() 時,函數
時,函數![]() 的最大值是
的最大值是![]() ,
,
對任意的![]() ,都存在
,都存在![]() ,
,
使得不等式![]() 成立,
成立,
等價于對任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
即對任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
記![]() ,
,
由![]() ,且
,且![]()
∴對任意的![]() ,不等式
,不等式![]() 都成立的必要條件為
都成立的必要條件為![]()
又![]() ,
,
由![]() 得
得![]() 或
或![]()
因為![]() ,所以
,所以![]() ,
,
當![]() 時,
時,![]() ,且
,且![]() 時,
時,![]() ,
,
![]() 時,
時,![]() ,所以
,所以![]() ,
,
所以![]() 時,
時,![]() 恒成立;
恒成立;
②當![]() 時,
時,![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
此時![]() 單調遞增,且
單調遞增,且![]() ,
,
所以![]() 時,
時,![]() 成立.
成立.
綜上,![]() 的取值范圍是
的取值范圍是![]()


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數學 來源: 題型:
【題目】如圖,平行四邊形![]() 所在平面與直角梯形
所在平面與直角梯形![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
,![]() 為
為![]() 中點.
中點.
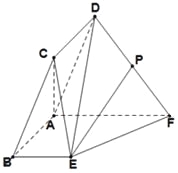
(1)求異面直線![]() 與
與![]() 所成的角;
所成的角;
(2)求平面![]() 與平面
與平面![]() 所成的二面角(銳角)的余弦值.
所成的二面角(銳角)的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側棱
中,側棱![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中點 .
的中點 .
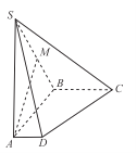
(Ⅰ)求證:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值;
所成銳二面角的余弦值;
(Ⅲ)設點![]() 是線段
是線段![]() 上的動點,
上的動點,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 分別為
分別為![]() 的中點,設直線
的中點,設直線![]() 與平面
與平面![]() 交于點
交于點![]() .
.

(1)已知平面![]() 平面
平面![]() ,求證:
,求證: ![]() .
.
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() ,圓
,圓![]() 是以
是以![]() 的中點為圓心,
的中點為圓心,![]() 為半徑的圓.
為半徑的圓.
(1)若圓![]() 的切線在
的切線在![]() 軸和
軸和![]() 軸上截距相等,求切線方程;
軸上截距相等,求切線方程;
(2)若![]() 是圓
是圓![]() 外一點,從
外一點,從![]() 向圓
向圓![]() 引切線
引切線![]() ,
,![]() 為切點,
為切點,![]() 為坐標原點,
為坐標原點,![]() ,求使
,求使![]() 最小的點
最小的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了解某地區觀眾對某類休育節目的收視情況,隨機抽取了100名觀眾進行調查,其中女性有55名.下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
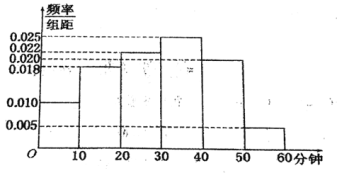
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”,已知“體育迷”中有10名女性.
(1)根據已知條件完成下面的![]() 列聯表,并據此資料判斷是否有
列聯表,并據此資料判斷是否有![]() 的把握認為“體育迷”與性別有關?
的把握認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | |||
合計 |
(2)將日均收看讀體育節目不低于50分鐘的觀眾稱為“超級體育迷”,已知“超級體育迷”中有2名女性,若從“超級體育迷”中任意選取2人,求至少有1名女性觀眾的概率.
附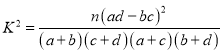 .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com