
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 分別為
分別為![]() 的中點,設直線
的中點,設直線![]() 與平面
與平面![]() 交于點
交于點![]() .
.

(1)已知平面![]() 平面
平面![]() ,求證:
,求證: ![]() .
.
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析(2)![]() .
.
【解析】試題分析:(1)由三角形中位線定理可得![]() ,利用線面平行的判定定理可得
,利用線面平行的判定定理可得![]() 平面
平面![]() ,在根據線面平行的性質定理可得
,在根據線面平行的性質定理可得![]() ;(2)由勾股定理可得
;(2)由勾股定理可得![]() , ∵
, ∵![]() 平面
平面![]() ,由此可以點
,由此可以點![]() 為原點,直線
為原點,直線![]() 分別為軸建立空間直角坐標系,利用兩直線垂直數量積為零列出方程組,分別求出直線
分別為軸建立空間直角坐標系,利用兩直線垂直數量積為零列出方程組,分別求出直線![]() 的方向向量與平面
的方向向量與平面![]() 的法向量,利用空間向量夾角余弦公式.
的法向量,利用空間向量夾角余弦公式.
試題解析:(1)∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∴![]() .
.
(2)∵底面是菱形, ![]() 為
為![]() 的中點
的中點![]() ∴
∴![]()
∴![]() ∵
∵![]() 平面
平面![]() ,則以點
,則以點![]() 為原點,直線
為原點,直線![]() 分別為軸建立如圖所示空間直角坐標系則
分別為軸建立如圖所示空間直角坐標系則![]()
∴![]() ,
, ![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,有
,有![]() 得
得![]()
設![]() ,則
,則![]() ,
, ![]()
則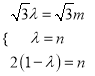 解之得
解之得![]() ,∴
,∴![]() ,
,
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]()
則![]()
∴直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
【方法點晴】本題主要考查線面平行的性質與判定以及利用空間向量求線面角,屬于難題. 空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】(導學號:05856307)(12分)
某老師為了分析學生的學習情況,隨機抽取了班上20名學生某次期末考試的成績(滿分為150分)進行分析,統計如下:
男生:133 131 130 126 123 120 116 109 107 105
女生:136 127 125 123 119 118 117 114 113 108
(Ⅰ)計算男、女生成績的平均值并分析比較男、女生成績的分散程度;
(Ⅱ)現從分數在120分以下的女同學中隨機抽取2位,求這兩位同學分數之差的絕對值小于10的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年10月份鄭州市進行了高三學生的體育學業水平測試,為了考察高中學生的身體素質比情況,現抽取了某校1000名(男生800名,女生200名)學生的測試成績,根據性別按分層抽樣的方法抽取100名進行分析,得到如下統計圖表:
男生測試情況:
抽樣情況 | 病殘免試 | 不合格 | 合格 | 良好 | 優秀 |
人數 | 5 | 10 | 15 | 47 |
|
女生測試情況
抽樣情況 | 病殘免試 | 不合格 | 合格 | 良好 | 優秀 |
人數 | 2 | 3 | 10 |
| 2 |
(1)現從抽取的1000名且測試等級為“優秀”的學生中隨機選出兩名學生,求選出的這兩名學生恰好是一男一女的概率;
(2)若測試等級為“良好”或“優秀”的學生為“體育達人”,其它等級的學生(含病殘免試)為“非體育達人”,根據以上統計數據填寫下面列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為體育達人”與性別有關?
男性 | 女性 | 總計 | |
體育達人 | |||
非體育達人 | |||
總計 |
臨界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附:(  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A是函數y=lg(20﹣8x﹣x2)的定義域,集合B是不等式x2﹣2x+1﹣a2≥0(a>0)的解集,p:x∈A,q:x∈B.
(1)若A∩B=,求實數a的取值范圍;
(2)若¬p是q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且以兩焦點為直徑的圓的內接正方形面積為2.
,且以兩焦點為直徑的圓的內接正方形面積為2.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() :
: ![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
, ![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() ,使直線
,使直線![]() 與
與![]() 的斜率之和
的斜率之和![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 坐標及該定值,若不存在,試說明理由.
坐標及該定值,若不存在,試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com