
【題目】已知圓O:![]() ,直線l:
,直線l:![]() .
.
![]() 若直線l與圓O交于不同的兩點(diǎn)A、B,當(dāng)
若直線l與圓O交于不同的兩點(diǎn)A、B,當(dāng)![]() 為銳角時(shí),求k的取值范圍;
為銳角時(shí),求k的取值范圍;
![]() 若
若![]() ,P是直線l上的動(dòng)點(diǎn),過P作圓O的兩條切線PC、PD,切點(diǎn)為C、D,則直線CD是否過定點(diǎn)?若是,求出定點(diǎn),并說明理由.
,P是直線l上的動(dòng)點(diǎn),過P作圓O的兩條切線PC、PD,切點(diǎn)為C、D,則直線CD是否過定點(diǎn)?若是,求出定點(diǎn),并說明理由.
![]() 若EF、GH為圓O的兩條相互垂直的弦,垂足為
若EF、GH為圓O的兩條相互垂直的弦,垂足為![]() ,求四邊形EGFH的面積的最大值.
,求四邊形EGFH的面積的最大值.
【答案】(1)![]() 或
或![]() ;(2)直線CD恒過定點(diǎn)
;(2)直線CD恒過定點(diǎn)![]() .詳見解析(3)
.詳見解析(3)![]()
【解析】
(1)首先可以設(shè)出![]() 兩點(diǎn)坐標(biāo),然后聯(lián)立圓與直線方程并得出
兩點(diǎn)坐標(biāo),然后聯(lián)立圓與直線方程并得出![]() 的值,最后根據(jù)
的值,最后根據(jù)![]() 以及
以及![]() 即可得出結(jié)果;
即可得出結(jié)果;
(2)首先將![]() 帶入直線方程得出直線的解析式,然后設(shè)出
帶入直線方程得出直線的解析式,然后設(shè)出![]() 點(diǎn)坐標(biāo)并寫出以
點(diǎn)坐標(biāo)并寫出以![]() 為直徑的圓的方程,最后將其與圓
為直徑的圓的方程,最后將其與圓![]() 方程聯(lián)立即可得出直線
方程聯(lián)立即可得出直線![]() 的方程并根據(jù)直線
的方程并根據(jù)直線![]() 的方程得出定點(diǎn)坐標(biāo);
的方程得出定點(diǎn)坐標(biāo);
(3)首先可以設(shè)圓心![]() 到直線
到直線![]() 的距離分別為
的距離分別為![]() 、
、![]() ,然后通過勾股定理即可得出
,然后通過勾股定理即可得出![]() 的值,再然后寫出
的值,再然后寫出![]() 與
與![]() ,通過
,通過![]() 即可求出四邊形
即可求出四邊形![]() 的面積的最大值。
的面積的最大值。
(1)根據(jù)題意,設(shè)![]() ,
,![]() ,
,
將![]() 代入
代入![]() ,整理得到:
,整理得到:![]() ,
,
則有![]() ,解可得:
,解可得:![]() ,
,
而![]() ,
,
![]() 為銳角
為銳角![]() ,
,
又由![]() ,
,
解可得:![]() ,
,
又由![]() ,則
,則![]() ,
,
解可得:![]() 或
或![]() ;
;
(2)![]() 時(shí),直線l的方程為:
時(shí),直線l的方程為:![]() ,
,
設(shè)![]() ,則以
,則以![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() ,
,
即![]() ,將其和圓O:
,將其和圓O:![]() 聯(lián)立,消去平方項(xiàng)得:
聯(lián)立,消去平方項(xiàng)得:![]() ,即為直線
,即為直線![]() 的方程,
的方程,
將其化為![]() 知該直線恒過定點(diǎn)
知該直線恒過定點(diǎn)![]() ,
,
故直線CD恒過定點(diǎn)![]() ;
;
(3)設(shè)圓心O到直線EF、GH的距離分別為![]() 、
、![]() ,
,
則![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
當(dāng)且僅當(dāng)![]() 即
即![]() 時(shí),取“
時(shí),取“![]() ”,
”,
所以四邊形EGFH的面積的最大值為![]() 。
。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,攝影愛好者在某公園A處,發(fā)現(xiàn)正前方B處有一立柱,測(cè)得立柱頂端O的仰角和立柱底部B的俯角均為![]() ,已知攝影愛好者的身高約為
,已知攝影愛好者的身高約為![]() 米(將眼睛S距地面的距離SA按
米(將眼睛S距地面的距離SA按![]() 米處理).
米處理).
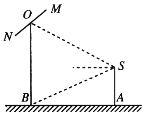
(1)求攝影愛好者到立柱的水平距離AB和立柱的高度OB;
(2)立柱的頂端有一長(zhǎng)為2米的彩桿MN,且MN繞其中點(diǎn)O在攝影愛好者與立柱所在的平面內(nèi)旋轉(zhuǎn).在彩桿轉(zhuǎn)動(dòng)的任意時(shí)刻,攝影愛好者觀察彩桿MN的視角![]() (設(shè)為
(設(shè)為![]() )是否存在最大值?若存在,請(qǐng)求出
)是否存在最大值?若存在,請(qǐng)求出![]() 取最大值時(shí)
取最大值時(shí)![]() 的值;若不存在,請(qǐng)說明理由.
的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一項(xiàng)是
其中第一項(xiàng)是![]() ,接下來的兩項(xiàng)是
,接下來的兩項(xiàng)是![]() ,
,![]() ,再接下來的三項(xiàng)是
,再接下來的三項(xiàng)是![]() ,
,![]() ,
,![]() ,依此類推那么該數(shù)列的前50項(xiàng)和為
,依此類推那么該數(shù)列的前50項(xiàng)和為![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱錐![]() 中,
中,![]() ,且
,且![]() 、
、![]() 、
、![]() 兩兩垂直,
兩兩垂直,![]() 是三棱錐
是三棱錐![]() 外接球面上一動(dòng)點(diǎn),則
外接球面上一動(dòng)點(diǎn),則![]() 到平面
到平面![]() 的距離的最大值是( )
的距離的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校為了解畢業(yè)班學(xué)業(yè)水平考試學(xué)生的數(shù)學(xué)考試情況,抽取了該校100名學(xué)生的數(shù)學(xué)成績(jī),將所有數(shù)據(jù)整理后,畫出了樣頻率分布直方圖(所圖所示),若第1組第9組的頻率各為x.

(1)求x的值,并估計(jì)這次學(xué)業(yè)水平考試數(shù)學(xué)成績(jī)的眾數(shù);
(2)若全校有1500名學(xué)生參加了此次考試,估計(jì)成績(jī)?cè)赱80,100)分內(nèi)的人數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若對(duì)任意的正整數(shù)![]() ,總存在正整數(shù)
,總存在正整數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() ,則稱
,則稱![]() 是“回歸數(shù)列”.
是“回歸數(shù)列”.
(![]() )①前
)①前![]() 項(xiàng)和為
項(xiàng)和為![]() 的數(shù)列
的數(shù)列![]() 是否是“回歸數(shù)列”?并請(qǐng)說明理由.②通項(xiàng)公式為
是否是“回歸數(shù)列”?并請(qǐng)說明理由.②通項(xiàng)公式為![]() 的數(shù)列
的數(shù)列![]() 是否是“回歸數(shù)列”?并請(qǐng)說明理由;
是否是“回歸數(shù)列”?并請(qǐng)說明理由;
(![]() )設(shè)
)設(shè)![]() 是等差數(shù)列,首項(xiàng)
是等差數(shù)列,首項(xiàng)![]() ,公差
,公差![]() ,若
,若![]() 是“回歸數(shù)列”,求
是“回歸數(shù)列”,求![]() 的值.
的值.
(![]() )是否對(duì)任意的等差數(shù)列
)是否對(duì)任意的等差數(shù)列![]() ,總存在兩個(gè)“回歸數(shù)列”
,總存在兩個(gè)“回歸數(shù)列”![]() 和
和![]() ,使得
,使得![]() 成立,請(qǐng)給出你的結(jié)論,并說明理由.
成立,請(qǐng)給出你的結(jié)論,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個(gè)盒中裝有編號(hào)分別為1,2,3,4的四個(gè)形狀大小完全相同的小球.
(1)從盒中任取兩球,求取出的球的編號(hào)之和大于5的概率.
(2)從盒中任取一球,記下該球的編號(hào)![]() ,將球放回,再從盒中任取一球,記下該球的編號(hào)
,將球放回,再從盒中任取一球,記下該球的編號(hào)![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A,B,C分別為△ABC的三邊a,b,c所對(duì)的角,向量![]() =(sin A,sin B),
=(sin A,sin B),![]() =(cos B,cos A),且
=(cos B,cos A),且![]() =sin 2C.
=sin 2C.
(1)求角C的大小;
(2)若sin A,sin C,sin B成等差數(shù)列,且![]() ,求邊c的長(zhǎng).
,求邊c的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,橢圓
中,橢圓![]() 的離心率為
的離心率為![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓
在橢圓![]() 上.
上.
![]() 求橢圓
求橢圓![]() 的方程;
的方程;
![]() 已知
已知![]() 與
與![]() 為平面內(nèi)的兩個(gè)定點(diǎn),過點(diǎn)
為平面內(nèi)的兩個(gè)定點(diǎn),過點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),求四邊形
兩點(diǎn),求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com