Question

【題目】已經(jīng)集合A={x|（8x﹣1）（x﹣1）≤0}；集合C={x|a＜x＜2a+5}
（1）若 ，求實數(shù)t的取值集合B；
（2）在（1）的條件下，若（A∪B）C，求實數(shù)a的取值范圍．

Answer 1

【答案】
（1）解：由已知集合A={x|（8x﹣1）（x﹣1）≤0}={x| ≤x≤1}

若 ，即| ≤（ ）t≤1，即2﹣3≤2﹣2t≤20

則﹣3≤﹣2t≤0，

即0≤t≤ ，故集合B=[0， ]

（2）解：在（1）的條件下，A∪B=[0， ]

由（A∪B）C，即[0， ]（a，2a+5），

∴ ，

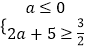解得：﹣ ≤a≤0

【解析】（1）求出集合A的等價條件，結(jié)合指數(shù)不等式的性質(zhì)進行求解即可．（2）根據(jù)集合的基本運算以及集合關(guān)系建立不等式關(guān)系進行求解即可．
【考點精析】解答此題的關(guān)鍵在于理解交、并、補集的混合運算的相關(guān)知識，掌握求集合的并、交、補是集合間的基本運算，運算結(jié)果仍然還是集合，區(qū)分交集與并集的關(guān)鍵是“且”與“或”，在處理有關(guān)交集與并集的問題時，常常從這兩個字眼出發(fā)去揭示、挖掘題設條件，結(jié)合Venn圖或數(shù)軸進而用集合語言表達，增強數(shù)形結(jié)合的思想方法．