
【題目】設首項為a1的正項數列{an}的前n項和為Sn,q為非零常數,已知對任意正整數n,m,Sn+m=Sm+qmSn總成立.
(1)求證:數列{an}是等比數列;
(2)若不等的正整數m,k,h成等差數列,試比較ammahh與ak2k的大小;
(3)若不等的正整數m,k,h成等比數列,試比較![]() 與
與![]() 的大小.
的大小.
【答案】(1)見解析(2)見解析(3)見解析
【解析】
(1)令n=m=1,得a2=qa1,令m=1,得Sn+1=S1+qSn(1),從而Sn+2=S1+qSn+1兩式相減即可得出an+2=qan+1,進而可判斷出數列{an}是等比數列
(2)根據m,k,h成等差數列,可知m+h=2k,進而可判定![]() ,進而根據等比數列的通項公式分q大于、等于和小于1三種情況判斷.
,進而根據等比數列的通項公式分q大于、等于和小于1三種情況判斷.
(3)正整數m,k,h成等比數列,則mh=k2,判斷出![]() ,進而根據等差根據等比數列的通項公式分a1和q大于、等于和小于1三種情況判斷.
,進而根據等差根據等比數列的通項公式分a1和q大于、等于和小于1三種情況判斷.
(1)證:因為對任意正整數n,m,Sn+m=Sm+qmSn總成立,
令n=m=1,得S2=S1+qS1,則a2=qa1
令m=1,得Sn+1=S1+qSn(1),從而Sn+2=S1+qSn+1(2),
(2)﹣(1)得an+2=qan+1,(n≥1)
綜上得an+1=qan(n≥1),所以數列{an}是等比數列
(2)正整數m,k,h成等差數列,
則m+h=2k,
所以![]() ,
,
則![]()
①當q=1時,ammahh=a12k=ak2k
②當q>1時,![]()
③當0<q<1時,![]()
(3)正整數m,k,h成等比數列,則mh=k2,則![]() ,
,
所以![]() ,
,![]()
①當a1=q,即![]() 時,
時,![]()
②當a1>q,即![]() 時,
時,![]()
③當a1<q,即![]() 時,
時,![]()


科目:高中數學 來源: 題型:
【題目】數據的收集和整理在當今社會起到了舉足輕重的作用,它用統計的方法來幫助人們分析以往的行為習慣,進而指導人們接下來的行動.
某支足球隊的主教練打算從預備球員甲、乙兩人中選一人為正式球員,他收集到了甲、乙兩名球員近期5場比賽的傳球成功次數,如下表:
場次 | 第一場 | 第二場 | 第三場 | 第四場 | 第五場 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
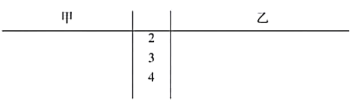
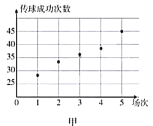
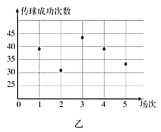
(1)根據這兩名球員近期5場比賽的傳球成功次數,完成莖葉圖(莖表示十位,葉表示個位);分別在平面直角坐標系中畫出兩名球員的傳球成功次數的散點圖;
(2)求出甲、乙兩名球員近期5場比賽的傳球成功次數的平均值和方差;
(3)主教練根據球員每場比賽的傳球成功次數分析出球員在場上的積極程度和技術水平,同時根據多場比賽的數據也可以分析出球員的狀態和潛力.你認為主教練應選哪位球員?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是橢圓
是橢圓![]() 上一動點,點
上一動點,點![]() 分別是左、右兩個焦點.
分別是左、右兩個焦點.![]() 面積的最大值為
面積的最大值為![]() ,且橢圓的長軸長為
,且橢圓的長軸長為![]() .
.
(1)求橢圓的標準方程;
(2)若點![]() ,
,![]() 在橢圓上,已知兩點
在橢圓上,已知兩點![]() ,
,![]() ,且以
,且以![]() 為直徑的圓經過坐標原點
為直徑的圓經過坐標原點![]() .求證:
.求證:![]() 的面積
的面積![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為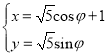 (φ為參數),以坐標原點O為極點,x軸的正半軸為極軸,建立極坐標系.
(φ為參數),以坐標原點O為極點,x軸的正半軸為極軸,建立極坐標系.
(1)求C1的極坐標方程;
(2)若C1與曲線C2:ρ=2sinθ交于A,B兩點,求|OA||OB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體![]() ,過對角線
,過對角線![]() 作平面
作平面![]() 交棱
交棱![]() 于點
于點![]() ,交棱
,交棱![]() 于點
于點![]() ,下列正確的是( )
,下列正確的是( )
A.平面![]() 分正方體所得兩部分的體積相等;
分正方體所得兩部分的體積相等;
B.四邊形![]() 一定是平行四邊形;
一定是平行四邊形;
C.平面![]() 與平面
與平面![]() 不可能垂直;
不可能垂直;
D.四邊形![]() 的面積有最大值.
的面積有最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的中點,
的中點,![]() ,將
,將![]() 沿
沿![]() 折起,得到四棱錐
折起,得到四棱錐![]() ,
,![]() 為
為![]() 的中點.
的中點.
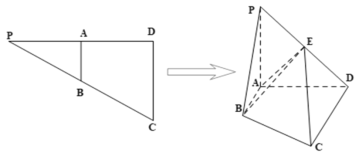
(1)證明:![]() 平面
平面![]() ;
;
(2)當正視圖方向與向量![]() 的方向相同時,此時
的方向相同時,此時![]() 的正視圖的面積為
的正視圖的面積為![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com