
【題目】判斷下列函數(shù)的奇偶性:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)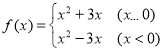
【答案】(1)非奇非偶;(2)既奇又偶;(3)非奇非偶;(4)非奇非偶;(5)偶;(6)奇;(7)奇;(8)偶
【解析】
先求函數(shù)的定義域,若定義域不關(guān)于原點對稱,則該函數(shù)是非奇非偶函數(shù);若定義域關(guān)于原點對稱,且![]() ,則該函數(shù)是既奇又偶函數(shù);若定義域關(guān)于原點對稱,再計算
,則該函數(shù)是既奇又偶函數(shù);若定義域關(guān)于原點對稱,再計算![]() ,看
,看![]() 與
與![]() 、
、![]() 是否相等,然后按照奇偶函數(shù)定義判斷;確定函數(shù)的定義域,有時能化簡函數(shù)的解析式,以便簡化解題過程,如(4)和(7)題;分段函數(shù)要分段分別判斷;根據(jù)以上逐一判斷即可.
是否相等,然后按照奇偶函數(shù)定義判斷;確定函數(shù)的定義域,有時能化簡函數(shù)的解析式,以便簡化解題過程,如(4)和(7)題;分段函數(shù)要分段分別判斷;根據(jù)以上逐一判斷即可.
解:(1)![]() ,其定義域不關(guān)于原點對稱,所以該函數(shù)是非奇非偶函數(shù);
,其定義域不關(guān)于原點對稱,所以該函數(shù)是非奇非偶函數(shù);
(2)根據(jù)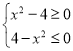 ,所以
,所以![]() 關(guān)于原點對稱,又
關(guān)于原點對稱,又![]()
![]() 是既奇又偶函數(shù);
是既奇又偶函數(shù);
(3)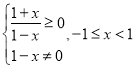 ,其定義域
,其定義域![]() 不關(guān)于原點對稱,
不關(guān)于原點對稱,
所以該函數(shù)是非奇非偶函數(shù);
(4)![]() 的定義域是
的定義域是![]() 不關(guān)于原點對稱,
不關(guān)于原點對稱,
所以該函數(shù)是非奇非偶函數(shù);
(5)![]() 的定義域是
的定義域是![]() 關(guān)于原點對稱,
關(guān)于原點對稱,
![]() ,所以該函數(shù)是偶函數(shù);
,所以該函數(shù)是偶函數(shù);
(6)![]() 的定義域是
的定義域是![]() 關(guān)于原點對稱
關(guān)于原點對稱
![]() ,所以該函數(shù)是奇函數(shù);
,所以該函數(shù)是奇函數(shù);
(7)![]() 定義域關(guān)于原點對稱,此時
定義域關(guān)于原點對稱,此時![]() ,
,
![]() ,所以該函數(shù)是奇函數(shù);
,所以該函數(shù)是奇函數(shù);
(8)函數(shù)定義域是![]() 關(guān)于原點對稱,
關(guān)于原點對稱,
當![]() ,則
,則![]() ,
,![]()
當![]() ,則
,則![]() ,
,![]()
![]() ,
,
所以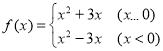 是偶函數(shù)
是偶函數(shù)


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】為選拔選手參加“中國詩詞大會”,某中學(xué)舉行一次“詩詞大賽”活動.為了了解本次競賽學(xué)生的成績情況,從中抽取了部分學(xué)生的分數(shù)(得分取正整數(shù),滿分為100分)作為樣本(樣本容量為![]() )進行統(tǒng)計.按照
)進行統(tǒng)計.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分組作出頻率分布直方圖,并作出樣本分數(shù)的莖葉圖(圖中僅列出了得分在
的分組作出頻率分布直方圖,并作出樣本分數(shù)的莖葉圖(圖中僅列出了得分在![]() ,
, ![]() 的數(shù)據(jù)).
的數(shù)據(jù)).
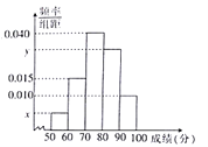
(1)求樣本容量![]() 和頻率分布直方圖中
和頻率分布直方圖中![]() 、
、![]() 的值;
的值;
(2)在選取的樣本中,從競賽成績在80分以上(含80分)的學(xué)生中隨機抽取2名學(xué)生參加“中國謎語大會”,設(shè)隨機變量![]() 表示所抽取的2名學(xué)生中得分在
表示所抽取的2名學(xué)生中得分在![]() 內(nèi)的學(xué)生人數(shù),求隨機變量
內(nèi)的學(xué)生人數(shù),求隨機變量![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某次考試結(jié)束,甲、乙、丙三位同學(xué)聚在一起聊天.甲說:“你們的成績都沒有我高![]() ”乙說:“我的成績一定比丙高
”乙說:“我的成績一定比丙高![]() ”丙說:“你們的成績都比我高
”丙說:“你們的成績都比我高![]() ”成績公布后,三人成績互不相同且三人中恰有一人說得不對,若將三人成績從高到低排序,則甲排在第______名
”成績公布后,三人成績互不相同且三人中恰有一人說得不對,若將三人成績從高到低排序,則甲排在第______名![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某少數(shù)民族的刺繡有著悠久的歷史,如圖4①,②,③,④為她們刺繡最簡單的四個圖案,這些圖案都是由小正方形構(gòu)成,小正方形數(shù)越多刺繡越漂亮.現(xiàn)按同樣的規(guī)律刺繡(小正方形的擺放規(guī)律相同),設(shè)第n個圖形包含f(n)個小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“歸納推理思想”,歸納出f(n+1)與f(n)之間的關(guān)系式,并根據(jù)你得到的關(guān)系式求出f(n)的表達式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)已知點A,B的坐標分別為(3,0),(-3,0),直線AP,BP相交于點P,且它們的斜率之積是-2,求動點P的軌跡方程.
(2)設(shè)P(x,y),直線l1:x+![]() y=0,l2:x-
y=0,l2:x-![]() y=0.若點P到l1的距離與點P到l2的距離之積為2,求動點P的軌跡方程.
y=0.若點P到l1的距離與點P到l2的距離之積為2,求動點P的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國家收購某種農(nóng)產(chǎn)品的價格為120元/t,其中征稅標準為每100元征收8元(稱稅率為8個百分點),計劃可收購a萬t,為減輕農(nóng)民負擔,決定降低稅率x個百分點,預(yù)計收購量可增加2x個百分點.
(1)寫出降低稅率后,稅收y(萬元)與x的關(guān)系式;
(2)要使此項稅收在稅率調(diào)整后不低于原計劃的78%,試確定x的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,圓錐PO中,AB是圓O的直徑,且AB=4,C是底面圓O上一點,且AC=2![]() ,點D為半徑OB的中點,連接PD.
,點D為半徑OB的中點,連接PD.
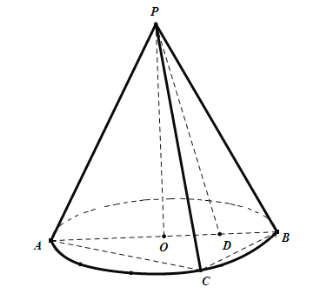
(1)求證:PC在平面APB內(nèi)的射影是PD;
(2)若PA=4,求底面圓心O到平面PBC的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知從1開始的連續(xù)奇數(shù)蛇形排列形成寶塔形數(shù)表,第一行為1,第二行為3,5,第三行為7,9,11,第四行為13,15,17,19,…,如圖所示,在寶塔形數(shù)表中位于第![]() 行、第
行、第![]() 列的數(shù)記為
列的數(shù)記為![]() ,比如
,比如![]() ,
,![]() ,
,![]() .若
.若![]() ,則
,則![]() ______.
______.
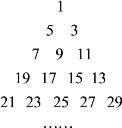
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
以平面直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,且兩個坐標系取相等的長度單位.已知直線
軸的正半軸為極軸,且兩個坐標系取相等的長度單位.已知直線![]() 的參數(shù)方程為
的參數(shù)方程為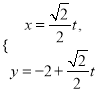 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為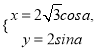 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 和
和![]() 的公共點的極坐標;
的公共點的極坐標;
(2)若![]() 為曲線
為曲線![]() 上的一個動點,求
上的一個動點,求![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com