
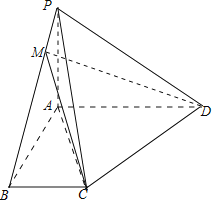
【題目】如圖,四棱錐P﹣ABCD中,已知PA⊥平面ABCD,△ABC為等邊三角形,PA=2AB=2,AC⊥CD,PD與平面PAC所成角的余弦值為![]() .
.
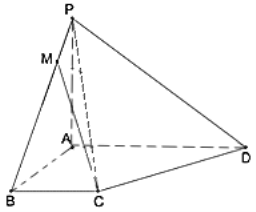
(1)證明:![]() 平面PAD;
平面PAD;
(2)點M為PB上一點,且![]() ,試判斷點M的位置.
,試判斷點M的位置.
【答案】(1)證明見解析.(2)點M的位置是靠近P的四等分點.
【解析】
(1)由PA⊥平面ABCD,得PA⊥CD,求解三角形證明∠CAD=60°,結合∠BCA=60°,得到BC∥AD,由直線與平面平行的判定可得BC∥平面PAD;
(2)設![]() ,則VM﹣PCD=λVB﹣PCD=λVP﹣BCD,求出三棱錐P﹣BCD的體積,結合
,則VM﹣PCD=λVB﹣PCD=λVP﹣BCD,求出三棱錐P﹣BCD的體積,結合![]() 求得λ值,可得點M的位置.
求得λ值,可得點M的位置.
(1)證明:∵PA⊥平面ABCD,∴PA⊥CD,
又AC⊥CD,CA∩PA=A,∴CD⊥平面PAC,
∴PD與平面PAC所成角為∠DPC,
在Rt△PCD中,cos∠DPC![]() ,
,
在Rt△PAC中,∵PC![]() ,∴PD=2
,∴PD=2![]() ,
,
在Rt△PAD中,∵PA=2,∴AD=2,
在Rt△ACD中,求得∠CAD=60°.
又∠BCA=60°,∴在平面ABCD中,得到BC∥AD,
而AD平面PAD,BC平面PAD,
∴BC∥平面PAD;
(2)解:∵點M在PB上,設![]() .
.
則VM﹣PCD=λVB﹣PCD=λVP﹣BCD,
∵![]() ,
,
∴![]() ,得
,得![]() .
.
∴點M的位置是靠近P的四等分點.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 的參數方程為
的參數方程為 (t為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)求曲線C上的點到![]() 距離的最大值及該點坐標.
距離的最大值及該點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一、高二年級的全體學生都參加了體質健康測試,測試成績滿分為![]() 分,規定測試成績在
分,規定測試成績在![]() 之間為“體質優秀”,在
之間為“體質優秀”,在![]() 之間為“體質良好”,在
之間為“體質良好”,在![]() 之間為“體質合格”,在
之間為“體質合格”,在![]() 之間為“體質不合格”.現從這兩個年級中各隨機抽取
之間為“體質不合格”.現從這兩個年級中各隨機抽取![]() 名學生,測試成績如下:
名學生,測試成績如下:
學生編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
高一年級 | 60 | 85 | 80 | 65 | 90 | 91 | 75 |
高二年級 | 79 | 85 | 91 | 75 | 60 |
|
|
其中![]() 是正整數.
是正整數.
(1)若該校高一年級有![]() 學生,試估計高一年級“體質優秀”的學生人數;
學生,試估計高一年級“體質優秀”的學生人數;
(2)若從高一年級抽取的![]() 名學生中隨機抽取
名學生中隨機抽取![]() 人,記
人,記![]() 為抽取的
為抽取的![]() 人中為“體質良好”的學生人數,求
人中為“體質良好”的學生人數,求![]() 的分布列及數學期望;
的分布列及數學期望;
(3)設兩個年級被抽取學生的測試成績的平均數相等,當高二年級被抽取學生的測試成績的方差最小時,寫出![]() 的值.(只需寫出結論)
的值.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法,如圖所示的程序框圖,給出了利用秦九韶算法求某多項式值的一個實例,若輸入x的值為2,則輸出![]() 的值為( )
的值為( )
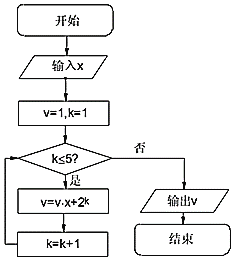
A.80B.192C.448D.36
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】陽馬和鱉臑(bienao)是《九章算術·商功》里對兩種錐體的稱謂.如圖所示,取一個長方體,按下圖斜割一分為二,得兩個模一樣的三棱柱,稱為塹堵(如圖).再沿其中一個塹堵的一個頂點與相對的棱剖開,得四棱錐和三棱錐各一個,有一棱與底面垂直的四棱錐稱為陽馬(四棱錐![]() )余下三棱錐稱為鱉臑(三棱錐
)余下三棱錐稱為鱉臑(三棱錐![]() )若將某長方體沿上述切割方法得到一個陽馬一個鱉臑,且該陽馬的正視圖和鱉臑的側視圖如圖所示,則可求出該陽馬和鱉臑的表面積之和為( )
)若將某長方體沿上述切割方法得到一個陽馬一個鱉臑,且該陽馬的正視圖和鱉臑的側視圖如圖所示,則可求出該陽馬和鱉臑的表面積之和為( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,國家相關政策大力鼓勵創新創業種植業戶小李便是受益者之一,自從2017年畢業以來,其通過自主創業而種植的某種農產品廣受市場青睞,他的種植基地也相應地新增加了一個平時小李便帶著部分員工往返于新舊基地之間進行科學管理和經驗交流,新舊基地之間開車單程所需時間為![]() ,由于不同時間段車流量的影響,現對50名員工往返新舊基地之間的用時情況進行統計,結果如下:
,由于不同時間段車流量的影響,現對50名員工往返新舊基地之間的用時情況進行統計,結果如下:
| 30 | 35 | 40 | 45 | 50 |
頻數(人) | 10 | 20 | 10 | 5 | 5 |
(1)若有50名員工參與調查,現從單程時間在35分鐘,40分鐘,45分鐘的人員中按分層抽樣的方法抽取7人,再從這7人中隨機抽取3人進行座談,用![]() 表示抽取的3人中時間在40分鐘的人數,求
表示抽取的3人中時間在40分鐘的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)某天,小李需要從舊基地駕車趕往新基地召開一個20分鐘的緊急會議,結束后立即返回舊基地.(以50名員工往返新舊基地之間的用時的頻率作為用時發生的概率)
①求小李從離開舊基地到返回舊基地共用時間不超過110分鐘的概率;
②若用隨機抽樣的方法從舊基地抽取8名骨干員工陪同小李前往新基地參加此次會議,其中有![]() 名員工從離開舊基地到返回舊基地共用時間不超過110分鐘,求隨機變量
名員工從離開舊基地到返回舊基地共用時間不超過110分鐘,求隨機變量![]() 的方差.
的方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】長沙市為了支援邊遠山區的教育事業,組織了一支由13名教師組成的隊伍下鄉支教,記者采訪隊長時詢問這個團隊的構成情況,隊長回答:“(1)有中學高級教師;(2)中學教師不多于小學教師;(3)小學高級教師少于中學中級教師;(4)小學中級教師少于小學高級教師;(5)支教隊伍的職稱只有小學中級、小學高級、中學中級、中學高級;(6)無論是否把我計算在內,以上條件都成立.”由隊長的敘述可以推測出他的學段及職稱分別是____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
,![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程
的極坐標方程![]() .
.
(1)若曲線![]() 與
與![]() 只有一個公共點,求
只有一個公共點,求![]() 的值;
的值;
(2)![]() 為曲線
為曲線![]() 上的兩點,且
上的兩點,且![]() ,求
,求![]() 的面積最大值.
的面積最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com