
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)估計該企業的職工對該部門評分不低于80的概率;
(3)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率.
的概率.
【答案】(Ⅰ)0.006;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】試題分析:(Ⅰ)在頻率分面直方圖中,由頻率總和即所有矩形面積之和為![]() ,可求
,可求![]() ;(Ⅱ)在頻率分布直方圖中先求出50名受訪職工評分不低于80的頻率為
;(Ⅱ)在頻率分布直方圖中先求出50名受訪職工評分不低于80的頻率為![]() ,由頻率與概率關系可得該部門評分不低于80的概率的估計值為
,由頻率與概率關系可得該部門評分不低于80的概率的估計值為![]() ;(Ⅲ)受訪職工評分在[50,60)的有3人,記為
;(Ⅲ)受訪職工評分在[50,60)的有3人,記為![]() ,受訪職工評分在[40,50)的有2 人,記為
,受訪職工評分在[40,50)的有2 人,記為![]() ,列出從這5人中選出兩人所有基本事件,即可求相應的概率.
,列出從這5人中選出兩人所有基本事件,即可求相應的概率.
試題解析:(Ⅰ)因為![]() ,所以
,所以![]() ……..4分)
……..4分)
(Ⅱ)由所給頻率分布直方圖知,50名受訪職工評分不低于80的頻率為![]() ,
,
所以該企業職工對該部門評分不低于80的概率的估計值為![]() ………8分
………8分
(Ⅲ)受訪職工評分在[50,60)的有:50×0.006×10=3(人),即為![]() ;
;
受訪職工評分在[40,50)的有: 50×0.004×40=2(人),即為![]() .
.
從這5名受訪職工中隨機抽取2人,所有可能的結果共有10種,它們是![]()
![]() 又因為所抽取2人的評分都在[40,50)的結果有1種,即
又因為所抽取2人的評分都在[40,50)的結果有1種,即![]() ,故所求的概率為
,故所求的概率為![]()


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】為鼓勵應屆畢業大學生自主創業,國家對應屆畢業大學生創業貸款有貼息優惠政策,現有應屆畢業大學生甲貸款開小型超市,初期投入為72萬元,經營后每年的總收入為50萬元,該公司第![]() 年需要付出的超市維護和工人工資等費用為
年需要付出的超市維護和工人工資等費用為![]() 萬元,已知
萬元,已知![]() 為等差數列,相關信息如圖所示.
為等差數列,相關信息如圖所示.

(Ⅰ)求![]() ;
;
(Ⅱ)該超市第幾年開始盈利?(即總收入減去成本及所有費用之差為正值)
(Ⅲ)該超市經營多少年,其年平均獲利最大?最大值是多少?(年平均獲利![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人們生活水平的不斷提高,家庭理財越來越引起人們的重視.某一調查機構隨機調查了5個家庭的月收入與月理財支出(單位:元)的情況,如下表所示:
月收入 | 8 | 10 | 9 | 7 | 11 |
月理財支出 |
|
|
|
|
|
(I)在下面的坐標系中畫出這5組數據的散點圖;
(II)根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(III)根據(II)的結果,預測當一個家庭的月收入為![]() 元時,月理財支出大約是多少元?
元時,月理財支出大約是多少元?
(附:回歸直線方程![]() 中,
中, ,
,![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的多面體中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() 是
是![]() 的中點.
的中點.

(![]() )求證:
)求證:![]() .
.
(![]() )若
)若![]() 為線段
為線段![]() 上一點,且
上一點,且![]() ,求證:
,求證:![]() 平面
平面![]() .
.
(![]() )在棱
)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .若存在,指出點
.若存在,指出點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列![]() 中,已知
中,已知![]() ,且對于任意正整數n都有
,且對于任意正整數n都有![]() .
.
(1)令![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)求![]() 的通項公式;
的通項公式;
(3)設![]() 是一個正數,無論
是一個正數,無論![]() 為何值,都有一個正整數
為何值,都有一個正整數![]() 使
使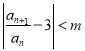 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
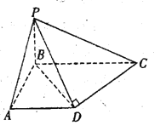
【題目】如圖,在四棱錐![]() 中,已知
中,已知![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,異面直線
,異面直線![]() 和
和![]() 所成角等于
所成角等于![]() .
.
(1)求直線![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角的正切值為
所成銳二面角的正切值為![]() ?若存在,指出點
?若存在,指出點![]() 在棱
在棱![]() 上的位置;若不存在,說明理由.
上的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列{![]() }的前n項和Sn=2
}的前n項和Sn=2![]() -2.
-2.
(1)求數列{![]() }的通項公式;
}的通項公式;
(2)若bn=![]() log
log![]()
![]() ,Sn=b1+b2+…+bn,對任意正整數n,Sn+(n+m)
,Sn=b1+b2+…+bn,對任意正整數n,Sn+(n+m)![]() <0恒成立,試求實數m的取值范圍.
<0恒成立,試求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 的圖像兩相鄰對稱軸之間的距離是
的圖像兩相鄰對稱軸之間的距離是![]() ,若將
,若將![]() 的圖像先向右平移
的圖像先向右平移![]() 個單位,再向上平移
個單位,再向上平移![]() 個單位,所得函數
個單位,所得函數![]() 為奇函數.
為奇函數.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的對稱軸及單調區間;
的對稱軸及單調區間;
(3)若對任意![]() ,
,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是一個容量為20的樣本數據分組后的頻率分布表:
分組 |
|
|
|
| ||
頻數 | 4 | 2 | 6 | 8 | ||
(1)請估計樣本的平均數;
(2)以頻率估計概率,若樣本的容量為2000,求在分組![]() 中的頻數;
中的頻數;
(3)若從數據在分組![]() 與分組
與分組![]() 的樣本中隨機抽取2個,求恰有1個樣本落在分組
的樣本中隨機抽取2個,求恰有1個樣本落在分組![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com