
【題目】已知拋物線![]() ,焦點為
,焦點為![]() ,點
,點![]() 在拋物線
在拋物線![]() 上,且
上,且![]() 到
到![]() 的距離比
的距離比![]() 到直線
到直線![]() 的距離小1.
的距離小1.
(1)求拋物線![]() 的方程;
的方程;
(2)若點![]() 為直線
為直線![]() 上的任意一點,過點
上的任意一點,過點![]() 作拋物線
作拋物線![]() 的切線
的切線![]() 與
與![]() ,切點分別為
,切點分別為![]() ,求證:直線
,求證:直線![]() 恒過某一定點.
恒過某一定點.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)根據(jù)拋物線定義可得直線![]() 為拋物線的準線,即得
為拋物線的準線,即得![]() ,(2)關(guān)鍵求出直線AB方程,先設(shè)切點
,(2)關(guān)鍵求出直線AB方程,先設(shè)切點![]() 的坐標,利用導數(shù)幾何意義可得切線斜率,進而根據(jù)點斜式可得切線方程,求兩切線方程交點可得點
的坐標,利用導數(shù)幾何意義可得切線斜率,進而根據(jù)點斜式可得切線方程,求兩切線方程交點可得點![]() 坐標,由于點
坐標,由于點![]() 在直線
在直線![]() 上,所以可得
上,所以可得![]() .最后聯(lián)立AB方程
.最后聯(lián)立AB方程![]() 與拋物線方程,利用韋達定理得
與拋物線方程,利用韋達定理得![]() ,即得直線
,即得直線![]() 恒過定點
恒過定點![]() .
.
試題解析:(1)因為![]() 到
到![]() 的距離與
的距離與![]() 到直線
到直線![]() 的距離相等,由拋物線定義知,直線
的距離相等,由拋物線定義知,直線![]() 為拋物線的準線,所以
為拋物線的準線,所以![]() ,得
,得![]() ,所以拋物線
,所以拋物線![]() 的方程為
的方程為![]() .
.
(2)設(shè)切點![]() 的坐標分別為
的坐標分別為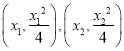 ,由(1)知,
,由(1)知, ![]() .
.
則切線![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,
故切線![]() 的方程分別為
的方程分別為![]() ,
, ![]() ,
,
聯(lián)立以上兩個方程,得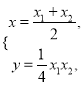 故
故![]() 的坐標為
的坐標為![]() .
.
因為點![]() 在直線
在直線![]() 上,所以
上,所以![]() ,即
,即![]() .
.
設(shè)直線![]() 的方程為
的方程為![]() ,代入拋物線方程
,代入拋物線方程![]() ,得
,得![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() .
.
故![]() 的方程為
的方程為![]() ,故直線
,故直線![]() 恒過定點
恒過定點![]() .
.


科目:高中數(shù)學 來源: 題型:
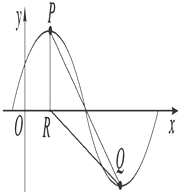
【題目】已知函數(shù)f(x)=Asin( ![]() x+φ),x∈R,A>0,0<φ<
x+φ),x∈R,A>0,0<φ< ![]() .y=f(x)的部分圖象如圖所示,P、Q 分別為該圖象的最高點和最低點,點P的坐標為(1,A).點R的坐標為(1,0),∠PRQ=
.y=f(x)的部分圖象如圖所示,P、Q 分別為該圖象的最高點和最低點,點P的坐標為(1,A).點R的坐標為(1,0),∠PRQ= ![]() .
. 
(1)求f(x)的最小正周期以及解析式.
(2)用五點法畫出f(x)在x∈[﹣ ![]() ,
, ![]() ]上的圖象.
]上的圖象.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在下列四個正方體中,![]() 為正方體的兩個頂點,
為正方體的兩個頂點,![]() 為所在棱的中點,則在這四個正方體中,直接
為所在棱的中點,則在這四個正方體中,直接![]() 與平面
與平面![]() 不平行的是( )
不平行的是( )
A. 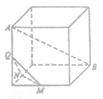 B.
B. 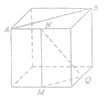
C. 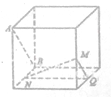 D.
D. 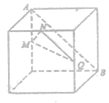
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 為實數(shù))的圖像在點
為實數(shù))的圖像在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求實數(shù)![]() 的值及函數(shù)
的值及函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè)函數(shù)![]() ,證明
,證明![]() 時,
時, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】將一個骰子先后拋擲兩次,事件![]() 表示:“第一次出現(xiàn)奇數(shù)點”,事件
表示:“第一次出現(xiàn)奇數(shù)點”,事件![]() 表示“第二次的點數(shù)不小于5”,則
表示“第二次的點數(shù)不小于5”,則![]() __________.
__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
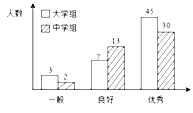
【題目】傳承傳統(tǒng)文化再掀熱潮,央視科教頻道以詩詞知識競賽為主的《中國詩詞大會》火爆熒屏。將中學組和大學組的參賽選手按成績分為優(yōu)秀、良好、一般三個等級,隨即從中抽取了100名選手進行調(diào)查,下面是根據(jù)調(diào)查結(jié)果繪制的選手等級人數(shù)的條形圖.
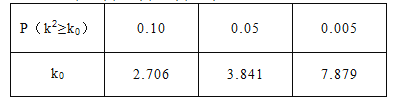
(Ⅰ)若將一般等級和良好等級合稱為合格等級,根據(jù)已知條件完成下面的![]() 列聯(lián)表,并據(jù)此資料你是否有95%的把握認為選手成績“優(yōu)秀”與文化程度有關(guān)?
列聯(lián)表,并據(jù)此資料你是否有95%的把握認為選手成績“優(yōu)秀”與文化程度有關(guān)?
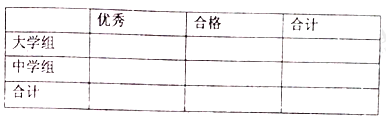
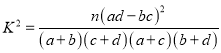 注:其中
注:其中![]() .
.
(Ⅱ)在優(yōu)秀等級的選手中取6名,依次編號為1,2,3,4,5,6,在良好等級的選手中取6名,依次編號為1,2,3,4,5,6,在選出的6名優(yōu)秀等級的選手中任取一名,記其編號為![]() ,在選出的6名良好等級的選手中任取一名,記其編號為
,在選出的6名良好等級的選手中任取一名,記其編號為![]() ,求使得方程組
,求使得方程組![]() 有唯一一組實數(shù)解
有唯一一組實數(shù)解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
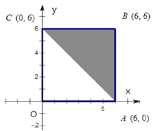
【題目】如圖:區(qū)域A是正方形OABC(含邊界),區(qū)域B是三角形ABC(含邊界)。
(Ⅰ)向區(qū)域A隨機拋擲一粒黃豆,求黃豆落在區(qū)域B的概率;
(Ⅱ)若x,y分別表示甲、乙兩人各擲一次骰子所得的點數(shù),求點(x,y)落在區(qū)域B的概率;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓方程![]() ,其左焦點、上頂點和左頂點分別為
,其左焦點、上頂點和左頂點分別為![]() ,
, ![]() ,
, ![]() ,坐標原點為
,坐標原點為![]() ,且線段
,且線段![]() ,
, ![]() ,
, ![]() 的長度成等差數(shù)列.
的長度成等差數(shù)列.
(Ⅰ)求橢圓的離心率;
(Ⅱ)若過點![]() 的一條直線
的一條直線![]() 交橢圓于點
交橢圓于點![]() ,
, ![]() ,交
,交![]() 軸于點
軸于點![]() ,使得線段
,使得線段![]() 被點
被點![]() ,
, ![]() 三等分,求直線
三等分,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com