
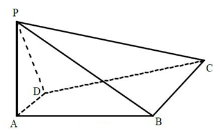
【題目】如圖,四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() .
.![]() ,
,![]() .
.
(1)求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(2)若平面![]() 內有一經過點
內有一經過點![]() 的曲線
的曲線![]() ,該曲線上的任一動點
,該曲線上的任一動點![]() 都滿足
都滿足![]() 與
與![]() 所成角的大小恰等于
所成角的大小恰等于![]() 與
與![]() 所成角.試判斷曲線
所成角.試判斷曲線![]() 的形狀并說明理由;
的形狀并說明理由;
(3)在平面![]() 內,設點
內,設點![]() 是(2)題中的曲線
是(2)題中的曲線![]() 在直角梯形
在直角梯形![]() 內部(包括邊界)的一段曲線
內部(包括邊界)的一段曲線![]() 上的動點,其中
上的動點,其中![]() 為曲線
為曲線![]() 和
和![]() 的交點.以
的交點.以![]() 為圓心,
為圓心,![]() 為半徑
為半徑![]() 的圓分別與梯形的邊
的圓分別與梯形的邊![]() 、
、![]() 交于
交于![]() 、
、![]() 兩點.當
兩點.當![]() 點在曲線段
點在曲線段![]() 上運動時,試求圓半徑
上運動時,試求圓半徑![]() 的范圍及
的范圍及![]() 的范圍.
的范圍.
【答案】(1)![]() ;(2)雙曲線;(3)
;(2)雙曲線;(3)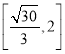 ,
,![]() .
.
【解析】
試題分析:(1)借助題設條件建立空間直角坐標系運用向量的數量積公式求解;(2)在空間坐標系中借助題設建立方程探求;(3)依據題設建立函數關系,運用二次函數的知識及不等式的性質等知識分析探求.
試題解析:
(1)如圖,以![]() 為原點,直線
為原點,直線![]() 為
為![]() 軸、直線
軸、直線![]() 為
為![]() 軸、直線
軸、直線![]() 為
為![]() 軸,建立空間直角坐標系.于是有
軸,建立空間直角坐標系.于是有![]() 、
、![]() ,則有
,則有![]() ,又
,又![]()
則異面直線![]() 與
與![]() 所成角
所成角![]() 滿足
滿足 ,
,
所以,異面直線![]() 與
與![]() 所成角的大小為
所成角的大小為![]() .
.
(2)如圖,以![]() 為原點,直線
為原點,直線![]() 為
為![]() 軸、直線
軸、直線![]() 為
為![]() 軸、直線
軸、直線![]() 為
為![]() 軸,建立空間直角坐標系.設點
軸,建立空間直角坐標系.設點![]() ,點
,點![]() 、點
、點![]() 、點
、點![]() ,
,
則![]() ,
,![]() ,
,
則![]() ,
,
![]() ,
,
化簡整理得到![]() ,
,
則曲線![]() 是平面
是平面![]() 內的雙曲線.
內的雙曲線.
(3)解:在如圖所示的![]() 的坐標系中,因為
的坐標系中,因為![]() 、
、![]() 、
、![]() ,設
,設![]() .則有
.則有![]() ,故
,故![]() 的方程為
的方程為![]() ,
,
代入雙曲線![]() :
:![]() 的方程可得,
的方程可得,![]() ,其中
,其中![]() .
.
因為直線![]() 與雙曲線
與雙曲線![]() 交于點
交于點![]() ,故
,故![]() .進而可得
.進而可得![]() ,即
,即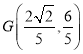 .故雙曲線
.故雙曲線![]() 在直角梯形
在直角梯形![]() 內部(包括邊界)的區域滿足
內部(包括邊界)的區域滿足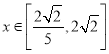 ,
,![]() .又設
.又設![]() 為雙曲線
為雙曲線![]() 上的動點,
上的動點,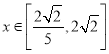 .
.
所以,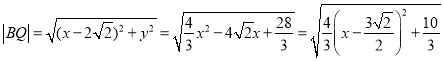
因為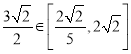 ,所以當
,所以當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .
.
而要使圓![]() 與
與![]() 、
、![]() 都有交點,則
都有交點,則![]() .
.
故滿足題意的圓的半徑取值范圍是 .
.
因為![]() ,所以
,所以![]() 體積為
體積為![]() .故問題可以轉化為研究
.故問題可以轉化為研究![]() 的面積.又因為
的面積.又因為![]() 為直角,所以
為直角,所以![]() 必為等腰直角三角形.
必為等腰直角三角形.
由前述,設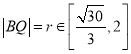 ,則
,則![]() ,
,
故其面積![]() ,所以
,所以![]() .
.
于是,![]() .
.
(當![]() 點運動到與點
點運動到與點![]() 重合時,體積取得最大值;當
重合時,體積取得最大值;當![]() 點運動到橫坐標
點運動到橫坐標![]() 時,即
時,即![]() 長度最小時,體積取得最小值)
長度最小時,體積取得最小值)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
: ![]() ,焦點
,焦點![]() ,
, ![]() 為坐標原點,直線
為坐標原點,直線![]() (不垂直
(不垂直![]() 軸)過點
軸)過點![]() 且與拋物線
且與拋物線![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若![]() 為線段
為線段![]() 的中點,射線
的中點,射線![]() 交拋物線
交拋物線![]() 于點
于點![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
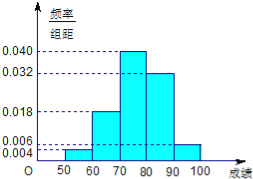
【題目】某班50名學生在一次數學測試中,成績全部介于50與100之間,將測試結果按如下方式分成五組:第一組[50,60),第二組[60,70),…,第五組[90,100].如圖所示是按上述分組方法得到的頻率分布直方圖.
(Ⅰ)若成績大于或等于60且小于80,認為合格,求該班在這次數學測試中成績合格的人數;
(Ⅱ)從測試成績在[50,60)∪[90,100]內的所有學生中隨機抽取兩名同學,設其測試成績分別為m、n,求事件“|m﹣n|>10”概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2009年推出一種新型家用轎車,購買時費用為![]() 萬元,每年應交付保險費、養路費及汽油費共
萬元,每年應交付保險費、養路費及汽油費共![]() 萬元,汽車的維修費為:第一年無維修費用,第二年為
萬元,汽車的維修費為:第一年無維修費用,第二年為![]() 萬元,從第三年起,每年的維修費均比上一年增加
萬元,從第三年起,每年的維修費均比上一年增加![]() 萬元.
萬元.
(1)設該輛轎車使用![]() 年的總費用(包括購買費用、保險費、養路費、汽油費及維修費)為
年的總費用(包括購買費用、保險費、養路費、汽油費及維修費)為![]() ,求
,求![]() 的表達式;
的表達式;
(2)這種汽車使用多少年報廢最合算(即該車使用多少年,年平均費用最少)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com