
【題目】《九章算術(shù)》卷五《商功》中有如下敘述“今有芻甍,下廣三丈,袤四丈,上袤二丈,無(wú)廣,高一丈“芻甍”指的是底面為矩形的對(duì)稱型屋脊?fàn)畹膸缀误w,“下廣三丈”是指底面矩形寬三丈,“袤四丈”是指底面矩形長(zhǎng)四丈,“上袤二丈”是指脊長(zhǎng)二丈,“無(wú)寬”是指脊無(wú)寬度,“高一丈”是指幾何體的高為一丈.現(xiàn)有一個(gè)芻甍如圖所示,下廣三丈,袤四丈,上袤三丈,無(wú)廣,高二丈,則該芻甍的外接球的表面積為_______________平方丈.


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 為坐標(biāo)原點(diǎn),雙曲線
為坐標(biāo)原點(diǎn),雙曲線![]()
![]() 上有
上有![]() 兩點(diǎn)滿足
兩點(diǎn)滿足![]() ,且點(diǎn)
,且點(diǎn)![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 處有極值
處有極值![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若關(guān)于![]() 的不等式
的不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在定義域上不單調(diào),求
在定義域上不單調(diào),求![]() 的取值范圍;
的取值范圍;
(2)設(shè)![]() 分別是
分別是![]() 的極大值和極小值,且
的極大值和極小值,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】第七屆世界軍人運(yùn)動(dòng)會(huì)(7th CISM Military World Games) ,簡(jiǎn)稱"武漢軍運(yùn)會(huì)”,于2019年10月18日至27日在中國(guó)武漢舉行,共設(shè)置射擊、游泳、田徑籃球等27個(gè)大項(xiàng)、329個(gè)小項(xiàng).來(lái)自100多個(gè)國(guó)家的近萬(wàn)名現(xiàn)役軍人同臺(tái)競(jìng)技.會(huì)議期間,某公司欲采購(gòu)海南某水果種植基地的水果,公司王總經(jīng)理與該種植基地的負(fù)責(zé)人張老板商定一次性采購(gòu)一種水果的采購(gòu)價(jià)![]() (千元/噸)與采購(gòu)量
(千元/噸)與采購(gòu)量![]() (噸)之間的函數(shù)關(guān)系的圖象如圖中的折線
(噸)之間的函數(shù)關(guān)系的圖象如圖中的折線![]() 所示(不包含端點(diǎn)
所示(不包含端點(diǎn)![]() ,但包含端點(diǎn)
,但包含端點(diǎn)![]() ).
).

(1)求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)已知該水果種植基地種植該水果的成本是8千元/噸,那么王總經(jīng)理的采購(gòu)量為多少時(shí),該水果基地在這次買賣中所獲得利潤(rùn)![]() 最大?最大利潤(rùn)是多少?
最大?最大利潤(rùn)是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 且
且![]() .
.
(1)若函數(shù)![]() 在
在![]() 上恒有意義,求
上恒有意義,求![]() 的取值范圍;
的取值范圍;
(2)是否存在實(shí)數(shù)![]() ,使函數(shù)
,使函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上為增函數(shù),且最大值為
上為增函數(shù),且最大值為![]() ?若存在求出
?若存在求出![]() 的值,若不存在請(qǐng)說(shuō)明理由.
的值,若不存在請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下圖為某倉(cāng)庫(kù)一側(cè)墻面的示意圖,其下部是矩形ABCD,上部是圓弧AB,該圓弧所在的圓心為O,為了調(diào)節(jié)倉(cāng)庫(kù)內(nèi)的濕度和溫度,現(xiàn)要在墻面上開(kāi)一個(gè)矩形的通風(fēng)窗EFGH(其中E,F在圓弧AB上,G,H在弦AB上).過(guò)O作![]() ,交AB 于M,交EF于N,交圓弧AB于P,已知
,交AB 于M,交EF于N,交圓弧AB于P,已知![]() (單位:m),記通風(fēng)窗EFGH的面積為S(單位:
(單位:m),記通風(fēng)窗EFGH的面積為S(單位:![]() )
)
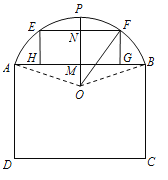
(1)按下列要求建立函數(shù)關(guān)系式:
(i)設(shè)![]() ,將S表示成
,將S表示成![]() 的函數(shù);
的函數(shù);
(ii)設(shè)![]() ,將S表示成
,將S表示成![]() 的函數(shù);
的函數(shù);
(2)試問(wèn)通風(fēng)窗的高度MN為多少時(shí),通風(fēng)窗EFGH的面積S最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在正方體ABCDA1B1C1D1中,設(shè)線段A1C與平面ABC1D1交于點(diǎn)Q,求證:B,Q,D1三點(diǎn)共線.
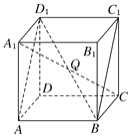
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,其中x>0,k為常數(shù),e為自然對(duì)數(shù)的底數(shù).
,其中x>0,k為常數(shù),e為自然對(duì)數(shù)的底數(shù).
(1)當(dāng)k≤0時(shí),求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 在區(qū)間(1,3)上存在兩個(gè)極值點(diǎn),求實(shí)數(shù)k的取值范圍;
在區(qū)間(1,3)上存在兩個(gè)極值點(diǎn),求實(shí)數(shù)k的取值范圍;
(3)證明:對(duì)任意給定的實(shí)數(shù)k,存在![]() (
(![]() ),使得
),使得![]() 在區(qū)間(
在區(qū)間(![]() ,
,![]() )上單調(diào)遞增.
)上單調(diào)遞增.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com