
【題目】設函數![]() ,其中x>0,k為常數,e為自然對數的底數.
,其中x>0,k為常數,e為自然對數的底數.
(1)當k≤0時,求![]() 的單調區間;
的單調區間;
(2)若函數![]() 在區間(1,3)上存在兩個極值點,求實數k的取值范圍;
在區間(1,3)上存在兩個極值點,求實數k的取值范圍;
(3)證明:對任意給定的實數k,存在![]() (
(![]() ),使得
),使得![]() 在區間(
在區間(![]() ,
,![]() )上單調遞增.
)上單調遞增.
【答案】(1)單調遞減區間為(0,3),單調遞增區間為![]() ;(2)
;(2)![]() ;(3)證明見解析。
;(3)證明見解析。
【解析】
(1)f′(x)=![]() .分別令f′(x)>0,f′(x)<0,解出x的取值范圍即可;
.分別令f′(x)>0,f′(x)<0,解出x的取值范圍即可;
(2)函數f(x)在(1,3)內存在兩個極值點,![]() 有兩個實數根.化為
有兩個實數根.化為![]() ,
,![]() ,因此
,因此![]() 在
在![]() 內存在兩個實數根.利用導數研究其單調性極值即可;
內存在兩個實數根.利用導數研究其單調性極值即可;
(3)令![]() ,得
,得![]() ,
,![]() 在
在![]() 上單調遞增,進而分析可得結果.
上單調遞增,進而分析可得結果.
![]() ,
,
(1)當![]() 時,
時,![]() 對任意的
對任意的![]() 都成立.
都成立.
所以,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以,![]() 的單調遞減區間為(0,3),單調遞增區間為
的單調遞減區間為(0,3),單調遞增區間為![]() .
.
(2)![]() 由函數
由函數![]() 在區間(1,3)上存在兩個極值點,得
在區間(1,3)上存在兩個極值點,得![]() 在區間(1,3)上至少有兩個解,即
在區間(1,3)上至少有兩個解,即![]() 在區間(1,3)至少有兩個解.
在區間(1,3)至少有兩個解.
令![]() ,
,![]() ,則
,則![]()
所以,當![]() 時,
時,![]() ;當
;當![]() ,
,![]() ,所以
,所以![]() 在區間(1,2)上單調遞減,在區間(2,3)上單調遞增.又
在區間(1,2)上單調遞減,在區間(2,3)上單調遞增.又![]() ,
,![]() ,
,
所以,![]() ,且
,且![]() ,即
,即![]() .
.
此時,存在x1∈(1,2), x2∈(2,3)使得![]()
且當x∈(1,x1)時,![]() ,當x∈(x1,x2)時,
,當x∈(x1,x2)時,![]() ,當x∈(x2,,3),
,當x∈(x2,,3),![]() ,滿足條件.
,滿足條件.
所以k的取值范圍為![]()
(3)令![]() ,得
,得![]() ,當
,當![]() 時,
時,![]() ,當且僅當
,當且僅當![]() 時等號成立,
時等號成立,
所以,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以,當![]() 時,
時,![]() ,及
,及![]() ,
,
當![]() 時,
時,![]() .
.
設![]() 為3和
為3和![]() 中較大的數,則當
中較大的數,則當![]() 時,
時,![]() ,
,
所以對任意給定的實數![]() ,存在
,存在![]() ,式得
,式得![]() 在區間
在區間![]() 上單調遞增.
上單調遞增.


科目:高中數學 來源: 題型:
【題目】《九章算術》卷五《商功》中有如下敘述“今有芻甍,下廣三丈,袤四丈,上袤二丈,無廣,高一丈“芻甍”指的是底面為矩形的對稱型屋脊狀的幾何體,“下廣三丈”是指底面矩形寬三丈,“袤四丈”是指底面矩形長四丈,“上袤二丈”是指脊長二丈,“無寬”是指脊無寬度,“高一丈”是指幾何體的高為一丈.現有一個芻甍如圖所示,下廣三丈,袤四丈,上袤三丈,無廣,高二丈,則該芻甍的外接球的表面積為_______________平方丈.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
如圖在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,點D是AB的
中點.
(1) 求證: AC⊥BC1
(2) 求證:AC1∥平面CDB1
(3) 求異面直線AC1與B1C所成角的余弦值.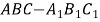
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某污水處理廠要在一個矩形污水處理池(ABCD)的池底水平鋪設污水凈化管道(管道構成Rt△FHE,H是直角項點)來處理污水.管道越長,污水凈化效果越好.設計要求管道的接口H是AB的中點,E,F分別落在線段BC,AD上.已知AB=20米,AD=![]() 米,記∠BHE=
米,記∠BHE=![]() .
.

(1)試將污水凈化管道的長度L表示為![]() 的函數,并寫出定義域;
的函數,并寫出定義域;
(2)當![]() 取何值時,污水凈化效果最好?并求出此時管道的長度L.
取何值時,污水凈化效果最好?并求出此時管道的長度L.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 、
、![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點.設不經過焦點
的左、右焦點.設不經過焦點![]() 的直線
的直線![]() 與橢圓交于兩個不同的點
與橢圓交于兩個不同的點![]() 、
、![]() ,焦點
,焦點![]() 到直線
到直線![]() 的距離為
的距離為![]() .若直線
.若直線![]() 、
、![]() 、
、![]() 的斜率依次成等差數列,求
的斜率依次成等差數列,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題不正確的是( )
A.研究兩個變量相關關系時,相關系數r為負數,說明兩個變量線性負相關
B.研究兩個變量相關關系時,相關指數R2越大,說明回歸方程擬合效果越好.
C.命題“x∈R,cosx≤1”的否定命題為“x0∈R,cosx0>1”
D.實數a,b,a>b成立的一個充分不必要條件是a3>b3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P和非零實數![]() ,若兩條不同的直線
,若兩條不同的直線![]() 均過點P,且斜率之積為
均過點P,且斜率之積為![]() ,則稱直線
,則稱直線![]() 是一組“
是一組“![]() 共軛線對”,如直
共軛線對”,如直![]() 是一組“
是一組“![]() 共軛線對”,其中O是坐標原點.
共軛線對”,其中O是坐標原點.
(1)已知![]() 是一組“
是一組“![]() 共軛線對”,求
共軛線對”,求![]() 的夾角的最小值;
的夾角的最小值;
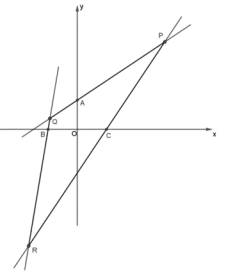
(2)已知點A(0,1)、點![]() 和點C(1,0)分別是三條直線PQ,QR,RP上的點(A,B,C與P,Q,R均不重合),且直線PR,PQ是“
和點C(1,0)分別是三條直線PQ,QR,RP上的點(A,B,C與P,Q,R均不重合),且直線PR,PQ是“![]() 共軛線對”,直線QP,QR是“
共軛線對”,直線QP,QR是“![]() 共軛線對”,直線RP,RQ是“
共軛線對”,直線RP,RQ是“![]() 共軛線對”,求點P的坐標;
共軛線對”,求點P的坐標;
(3)已知點![]() ,直線
,直線![]() 是“
是“![]() 共軛線對”,當
共軛線對”,當![]() 的斜率變化時,求原點O到直線
的斜率變化時,求原點O到直線![]() 的距離之積的取值范圍.
的距離之積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com