
��֪���タ(xi��n)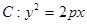 ���c(di��n)P��-1��0�������(zh��n)��(xi��n)�c
���c(di��n)P��-1��0�������(zh��n)��(xi��n)�c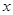 �S�Ľ��c(di��n)���^(gu��)P��ֱ��(xi��n)
�S�Ľ��c(di��n)���^(gu��)P��ֱ��(xi��n)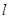 �c���タ(xi��n)C����A��B���c(di��n).
�c���タ(xi��n)C����A��B���c(di��n).
��1����(d��ng)��(xi��n)��AB�����c(di��n)��ֱ��(xi��n)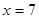 �ϕr(sh��)����ֱ��(xi��n)
�ϕr(sh��)����ֱ��(xi��n)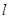 �ķ��̣�
�ķ��̣�
��2���O(sh��)F�钁�タ(xi��n)C�Ľ��c(di��n)����(d��ng)A�龀(xi��n)��PB���c(di��n)�r(sh��)�����FAB����e.
��1��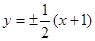 . ��2��
. ��2��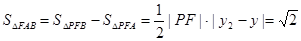 .
.
����ԇ�}��������1�����ȴ_�����タ(xi��n)���̞�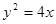 ����ֱ��(xi��n)
����ֱ��(xi��n)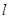 �ķ��̞�
�ķ��̞�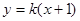 �������}��
�������}��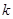 ���ڣ���
���ڣ���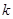 ��0���c���タ(xi��n)����(li��n)������ȥ
��0���c���タ(xi��n)����(li��n)������ȥ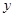 �Ñ�(y��ng)�����c(di��n)����(bi��o)��ʽAB���c(di��n)�ęM����(bi��o)��
�Ñ�(y��ng)�����c(di��n)����(bi��o)��ʽAB���c(di��n)�ęM����(bi��o)��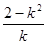 ���M(j��n)һ�����ֱ��(xi��n)��б�ʣ��Ķ��ɵ�ֱ��(xi��n)����.��(y��ng)ע��ֱ��(xi��n)б�ʵĴ�����.
���M(j��n)һ�����ֱ��(xi��n)��б�ʣ��Ķ��ɵ�ֱ��(xi��n)����.��(y��ng)ע��ֱ��(xi��n)б�ʵĴ�����.
��2������(j��)���c(di��n)����(bi��o)��ʽ�_���õ���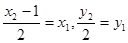 ������A��B�钁�タ(xi��n)���c(di��n)���õõ����̽M���
������A��B�钁�タ(xi��n)���c(di��n)���õõ����̽M���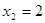 ��
��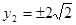 ��Ӌ(j��)��õ���FAB����e
��Ӌ(j��)��õ���FAB����e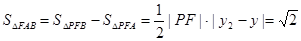 .ע��Y(ji��)�ψD�η�����ͨ�^(gu��)�_���c(di��n)������(bi��o)���õ������εĸ߾�(xi��n)�L(zh��ng).
.ע��Y(ji��)�ψD�η�����ͨ�^(gu��)�_���c(di��n)������(bi��o)���õ������εĸ߾�(xi��n)�L(zh��ng).
ԇ�}��������1����?y��n)钁�タ(xi��n)�Ĝ�(zh��n)��(xi��n)��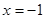 ������
������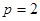 ��
��
���タ(xi��n)���̞�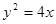 2��
2��
�O(sh��)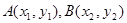 ��ֱ��(xi��n)
��ֱ��(xi��n)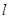 �ķ��̞�
�ķ��̞�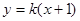 �������}��
�������}��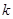 ���ڣ���
���ڣ���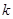 ��0���c���タ(xi��n)����(li��n)������ȥ
��0���c���タ(xi��n)����(li��n)������ȥ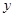 ��
��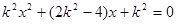 ��*��
��*��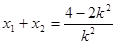 ��
��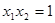 4��
4��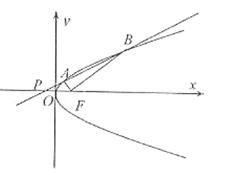
����AB���c(di��n)�ęM����(bi��o)��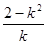 ����
����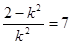 ������
������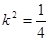 6��
6��
���˕r(sh��)��*��ʽ�Єeʽ�����㣩
����ֱ��(xi��n)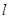 �ķ��̞�
�ķ��̞�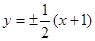 7��
7��
��2����?y��n)�A�龀(xi��n)��PB���c(di��n)������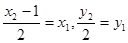 8��
8��
��A��B�钁�タ(xi��n)���c(di��n)����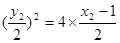 ��
�� 10��
10��
���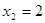 ��
��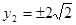 11��
11��
��(d��ng)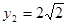 �r(sh��)��
�r(sh��)��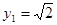 ����(d��ng)
����(d��ng)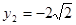 �r(sh��)��
�r(sh��)��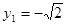 12��
12��
���ԡ�FAB����e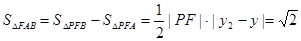 14��
14��
���c(di��n)�����タ(xi��n)��(bi��o)��(zh��n)���̣�ֱ��(xi��n)�c���タ(xi��n)��λ���P(gu��n)ϵ.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A�����Ğ�ԭ�c(di��n) ���L(zh��ng)�S�L(zh��ng)��
���L(zh��ng)�S�L(zh��ng)��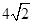 ��һ�l��(zh��n)��(xi��n)�ķ��̞�
��һ�l��(zh��n)��(xi��n)�ķ��̞�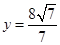 .
.
������ԓ�E�A�Ę�(bi��o)��(zh��n)���̣�
�����侀(xi��n)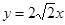
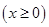 �c�E�A�Ľ��c(di��n)��
�c�E�A�Ľ��c(di��n)��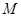 ���^(gu��)
���^(gu��)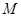 ���Aб�ǻ��a(b��)�ăɗlֱ��(xi��n)���քe�c�E�A����
���Aб�ǻ��a(b��)�ăɗlֱ��(xi��n)���քe�c�E�A����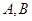 ���c(di��n)��
���c(di��n)��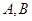 ���c(di��n)����
���c(di��n)����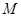 �������C��ֱ��(xi��n)
�������C��ֱ��(xi��n)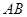 ��б�ʞ鶨ֵ��
��б�ʞ鶨ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A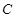 ��
��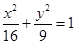 �c
�c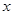 �����S��
�����S��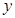 �����S�Ľ��c(di��n)�քe��
�����S�Ľ��c(di��n)�քe��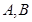 ����(d��ng)�c(di��n)
����(d��ng)�c(di��n)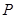 �ǙE�A����һ�c(di��n)����
�ǙE�A����һ�c(di��n)����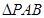 ��e�����ֵ��
��e�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A��������ԭ�c(di��n)�����c(di��n)�� �S�ϣ�������
�S�ϣ�������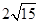 ���ҽ�(j��ng)�^(gu��)�c(di��n)
���ҽ�(j��ng)�^(gu��)�c(di��n)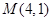 ��ֱ��(xi��n)
��ֱ��(xi��n)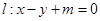 ���E�A�ڲ�ͬ�ă��c(di��n)A��B.
���E�A�ڲ�ͬ�ă��c(di��n)A��B.
(1)��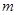 ��ȡֵ��������
��ȡֵ��������
(2)��ֱ��(xi��n)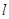 ����(j��ng)�^(gu��)�c(di��n)
����(j��ng)�^(gu��)�c(di��n)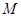 �����C��ֱ��(xi��n)
�����C��ֱ��(xi��n) ��б�ʻ����෴��(sh��).
��б�ʻ����෴��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)�E�A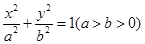 �����c(di��n)��
�����c(di��n)�� ���x���ʞ�
���x���ʞ�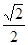 ���^(gu��)�c(di��n)
���^(gu��)�c(di��n) ���c
���c �S��ֱ��ֱ��(xi��n)���E�A�صõľ�(xi��n)���L(zh��ng)��
�S��ֱ��ֱ��(xi��n)���E�A�صõľ�(xi��n)���L(zh��ng)��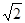 .
.
(1) ��E�A����.
(2) �^(gu��)�c(di��n)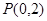 ��ֱ��(xi��n)
��ֱ��(xi��n)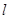 �c�E�A���ڲ�ͬ�ă��c(di��n)
�c�E�A���ڲ�ͬ�ă��c(di��n)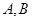 ����(d��ng)
����(d��ng)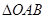 ��e���r(sh��)����
��e���r(sh��)����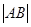 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪���E�AC�^(gu��)�c(di��n)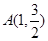 ���ɂ�(g��)���c(di��n)��
���ɂ�(g��)���c(di��n)��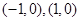 ��
��
(1)��E�AC�ķ��̣�
(2)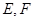 �ǙE�AC�ϵăɂ�(g��)��(d��ng)�c(di��n)�����ֱ��(xi��n)
�ǙE�AC�ϵăɂ�(g��)��(d��ng)�c(di��n)�����ֱ��(xi��n)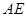 ��б���c
��б���c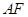 ��б�ʻ����෴��(sh��)���C��ֱ��(xi��n)
��б�ʻ����෴��(sh��)���C��ֱ��(xi��n)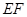 ��б�ʞ鶨ֵ��������@��(g��)��ֵ��
��б�ʞ鶨ֵ��������@��(g��)��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��)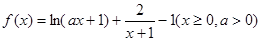 ��
��
��1����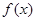 ��
��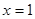 ̎ȡ�ØOֵ����
̎ȡ�ØOֵ���� ��ֵ��
��ֵ��
��2����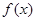 ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��3����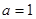 ��
��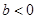 ������(sh��)
������(sh��)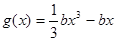 ����(du��)��
����(du��)��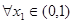 ��������
��������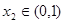 ʹ��
ʹ��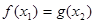 ����(sh��)��(sh��)
����(sh��)��(sh��) ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A�� ��
��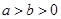 ��������һ�c(di��n)���ɽ��c(di��n)���x֮�͞�
��������һ�c(di��n)���ɽ��c(di��n)���x֮�͞�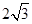 ���x���ʞ�
���x���ʞ�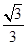 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��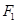 ��
��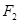 ���c(di��n)
���c(di��n)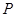 ���Ҝ�(zh��n)��(xi��n)������һ�c(di��n)���^(gu��)
���Ҝ�(zh��n)��(xi��n)������һ�c(di��n)���^(gu��)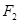 ��ֱ ��(xi��n)
��ֱ ��(xi��n)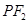 �Ĵ���(xi��n)
�Ĵ���(xi��n)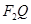 ���E�A��
���E�A��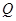 �c(di��n)��
�c(di��n)��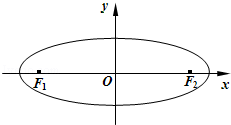
��1����E�A �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���C����ֱ��(xi��n)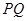 �cֱ��(xi��n)
�cֱ��(xi��n)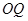 ��б��֮�e�Ƕ�ֵ��
��б��֮�e�Ƕ�ֵ��
��3���c(di��n)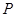 �Ŀv����(bi��o)��3���^(gu��)
�Ŀv����(bi��o)��3���^(gu��)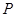 ����(d��ng)ֱ��(xi��n)
����(d��ng)ֱ��(xi��n)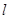 �c�E�A���ڃɂ�(g��)��ͬ�c(di��n)
�c�E�A���ڃɂ�(g��)��ͬ�c(di��n)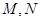 ���ھ�(xi��n)��
���ھ�(xi��n)��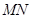 ��ȡ�c(di��n)
��ȡ�c(di��n)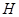 ���M(m��n)��
���M(m��n)��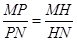 ��ԇ�C���c(di��n)
��ԇ�C���c(di��n)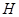 ����һ��ֱ��(xi��n)�ϣ�
����һ��ֱ��(xi��n)�ϣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��(d��ng)�c(di��n)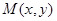 �c���c(di��n)
�c���c(di��n)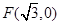 �ľ��x������ֱ��(xi��n)
�ľ��x������ֱ��(xi��n)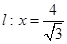 �ľ��x֮���dz���(sh��)
�ľ��x֮���dz���(sh��) ,ӛ�c(di��n)
,ӛ�c(di��n)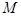 ��܉�E������(xi��n)
��܉�E������(xi��n) .
.
��I��������(xi��n) �ķ��̣�
�ķ��̣�
��II���O(sh��)ֱ��(xi��n)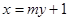 �c����(xi��n)
�c����(xi��n) ����
����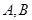 ���c(di��n)��
���c(di��n)�� ������(bi��o)ԭ�c(di��n)����
������(bi��o)ԭ�c(di��n)����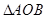 ��e�����ֵ��
��e�����ֵ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com