
【題目】已知函數f(x)=sin x,g(x)=mx-![]() (m為實數).
(m為實數).
(1)求曲線y=f(x)在點![]() 處的切線方程;
處的切線方程;
(2)求函數g(x)的單調遞減區間;
(3)若m=1,證明:當x>0時,f(x)<g(x)+![]() .
.
【答案】(1)x-![]() y+1-
y+1-![]() =0(2)見解析
=0(2)見解析
【解析】試題分析:(1)求出函數![]() 的導函數,求出
的導函數,求出![]() 得到切線的斜率,求出
得到切線的斜率,求出![]() 的值,求得切點坐標,由直線方程的點斜式得到切線方程;(2)求出函數
的值,求得切點坐標,由直線方程的點斜式得到切線方程;(2)求出函數![]() 的導函數
的導函數![]() ,然后討論
,然后討論![]() 和
和![]() 分析導函數的符號,從而求得
分析導函數的符號,從而求得![]() 的單調遞減區間;(3)分別構造函數
的單調遞減區間;(3)分別構造函數![]() ,
,
然后利用其導函數的符號判斷所構造函數的單調性,從而證明答案.
試題解析:(1)解 由題意得所求切線的斜率k=f′![]() =cos
=cos![]() =
=![]() .切點P
.切點P![]() ,則切線方程為y-
,則切線方程為y-![]() =
=![]()
![]() .即x-
.即x-![]() y+1-
y+1-![]() =0.
=0.
(2)解 g′(x)=m-![]() x2.
x2.
①當m≤0時,g′(x)≤0,則g(x)的單調遞減區間是(-∞,+∞);
②當m>0時,令g′ (x)<0,解得x<-![]() 或x>
或x>![]() ,則g(x)的單調遞減區間是(-∞,-
,則g(x)的單調遞減區間是(-∞,-![]() ),(
),(![]() ,+∞).
,+∞).
(3)證明 當m=1時,g(x)=x-![]() .
.
令h(x)=g(x)+![]() -f(x)=x-sin x,x∈[0,+∞),
-f(x)=x-sin x,x∈[0,+∞),
h′(x)=1-cos x≥0,則h(x)是[0,+∞)上的增函數.
故當x>0時,h(x)>h(0)=0,
即sin x<x,f(x)<g(x)+![]() .
.
【方法點晴】本題主要考查利用導數求曲線切線以及利用導數研究函數的單調性、分類討論思想的應用,屬于難題.求曲線切線方程的一般步驟是:(1)求出![]() 在
在![]() 處的導數,即
處的導數,即![]() 在點
在點![]()
![]() 出的切線斜率(當曲線
出的切線斜率(當曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行時,在 處導數不存在,切線方程為
軸平行時,在 處導數不存在,切線方程為![]() );(2)由點斜式求得切線方程
);(2)由點斜式求得切線方程![]() .
.


科目:高中數學 來源: 題型:
【題目】(2017·成都高中畢業第一次診斷)已知雙曲線![]() (a>0,b>0)的左、右焦點分別為F1,F2,雙曲線上一點P滿足PF2⊥x軸.若|F1F2|=12,|PF2|=5,則該雙曲線的離心率為( )
(a>0,b>0)的左、右焦點分別為F1,F2,雙曲線上一點P滿足PF2⊥x軸.若|F1F2|=12,|PF2|=5,則該雙曲線的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出集合![]() .
.
(1)若![]() ,求證:函數
,求證:函數![]() ;
;
(2)由(1)分析可知, ![]() 是周期函數且是奇函數,于是張三同學得出兩個命
是周期函數且是奇函數,于是張三同學得出兩個命
題:命題甲:集合![]() 中的元素都是周期函數.命題乙:集合
中的元素都是周期函數.命題乙:集合![]() 中的元素都是奇函數. 請對此
中的元素都是奇函數. 請對此
給出判斷,如果正確,請證明;如果不正確,請舉反例;
(3)若![]() ,數列
,數列![]() 滿足:
滿足: ![]() ,且
,且![]()
![]() ,數列
,數列![]() 的前
的前![]() 項
項
和為![]() ,試問是否存在實數
,試問是否存在實數![]() 、
、![]() ,使得任意的
,使得任意的![]() ,都有
,都有![]() 成立,若
成立,若
存在,求出![]() 、
、![]() 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在扶貧活動中,為了盡快脫貧(無債務)致富,企業甲將經營狀況良好的某種消費品專賣店以5.8萬元的優惠價格轉讓給了尚有5萬元無息貸款沒有償還的小型企業乙,并約定從該店經營的利潤中,首先保證企業乙的全體職工每月最低生活費的開支3 600元后,逐步償還轉讓費(不計息).在甲提供的資料中:①這種消費品的進價為每件14元;②該店月銷量Q(百件)與銷售價格P(元)的關系如圖所示;③每月需各種開支2 000元.
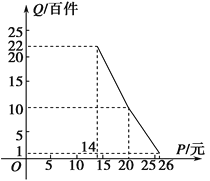
(1)當商品的價格為每件多少元時,月利潤扣除職工最低生活費的余額最大?并求最大余額;
(2)企業乙只依靠該店,最早可望在幾年后脫貧?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=4x和直線l:x=-1.
(1)若曲線C上存在一點Q,它到l的距離與到坐標原點O的距離相等,求Q點的坐標;
(2)過直線l上任一點P作拋物線的兩條切線,切點記為A,B,求證:直線AB過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】博鰲亞洲論壇2015年會員大會于3月27日在海南博鰲舉辦,大會組織者對招募的100名服務志愿者培訓后,組織一次![]() 知識競賽,將所得成績制成如右頻率分布直方圖(假定每個分數段內的成績均勻分布),組織者計劃對成績前20名的參賽者進行獎勵.
知識競賽,將所得成績制成如右頻率分布直方圖(假定每個分數段內的成績均勻分布),組織者計劃對成績前20名的參賽者進行獎勵.

(1)試確定受獎勵的分數線;
(2)從受獎勵的20人中利用分層抽樣抽取5人,再從抽取的5人中抽取2人在主會場服務,試求2人成績都在90分以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某項競賽分為初賽、復賽、決賽三個階段進行,每個階段選手要回答一個問題.規定正確回答問題者進入下一階段競賽,否則即遭淘汰.已知某選手通過初賽、復賽、決賽的概率分別是![]() 且各階段通過與否相互獨立.
且各階段通過與否相互獨立.
(1)求該選手在復賽階段被淘汰的概率;
(2)設該選手在競賽中回答問題的個數為ξ,求ξ的分布列與均值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com