【題目】已知函數
.
(Ⅰ)當a＝1時，求
的解集；
(Ⅱ)當
時， 
恒成立，求實數a的取值范圍．
【答案】(Ⅰ) 
；(Ⅱ) 
.
【解析】試題分析：（1）當a＝1時，利用零點分段法轉化為不含絕對值的不等式組即可；（2）根據所給范圍把不等式轉化為只含一個絕對值的不等式，再利用公式去掉絕對值，通過變量分離求最值即可.
試題解析：
(Ⅰ)原不等式可化為
＋
≤3，依題意，當x>2時，3x－3≤3，則x≤2，無解，
當
≤x≤2時，x＋1≤3，則x≤2，
所以≤x≤2，
當x<時，3－3x≤3，則x≥0，所以0≤x<，
綜上所述：原不等式的解集為
(Ⅱ)原不等式可化為
≤3－，因為x∈
，所以≤4－2x，
即2x－4≤2a－x≤4－2x，故3x－4≤2a≤4－x對x∈恒成立，
當1≤x≤2時，3x－4的最大值2,4－x的最小值為2，所以a的取值范圍為
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝sin x，g(x)＝mx－
(m為實數).
(1)求曲線y＝f(x)在點
處的切線方程；
(2)求函數g(x)的單調遞減區間；
(3)若m＝1，證明：當x＞0時，f(x)＜g(x)＋
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某人為研究中學生的性別與每周課外閱讀量這兩個變量的關系，隨機抽查了100名中學生，得到頻率分布直方圖(如圖所示)，其中樣本數據的分組區間為：[0,2]，(2,4]，(4,6]，(6,8]，(8,10]，(10,12]．
(Ⅰ)假設同一組中的每個數據可用該組區間的中點值代替，試估計樣本中的100名學生周課外閱讀時間的平均數．
(Ⅱ)在樣本數據中，有20位女生的每周課外閱讀時間超過4小時，15位男生的每周課外閱讀時間沒有超過4小時．請畫出每周課外閱讀時間與性別列聯表，并判斷能否在犯錯誤的概率不超過0.05的前提下認為“該校學生的每周課外閱讀時間與性別有關”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附：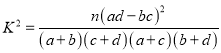 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2016·廣州模擬)如圖，在三棱柱ABC－A1B1C1中，側棱AA1⊥底面ABC，AB＝AC＝2AA1，∠BAC＝120°，D，D1分別是線段BC，B1C1的中點，過線段AD的中點P作BC的平行線，分別交AB，AC于點M，N.
(1)證明：MN⊥平面ADD1A1；
(2)求二面角A－A1M－N的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直三棱柱ABC－A1B1C1中，平面α與棱AB，AC，A1C1，A1B1分別交于點E，F，G，H，且直線AA1∥平面α.有下列三個命題：①四邊形EFGH是平行四邊形；②平面α∥平面BCC1B1；③平面α⊥平面BCFE.其中正確的命題有( )
A. ①② B. ②③
C. ①③ D. ①②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知{an}是等差數列，{bn}是各項均為正數的等比數列，且b1＝a1＝1，b3＝a4，b1＋b2＋b3＝a3＋a4.
(1)求數列{an}，{bn}的通項公式；
(2)設cn＝anbn，求數列{cn}的前n項和Tn.
查看答案和解析>>
科目：高中數學 來源： 題型：
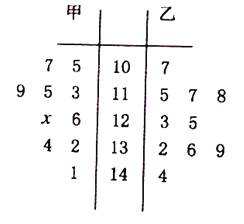
【題目】為了減少霧霾，還城市一片藍天，某市政府于12月4日到12月31日在主城區實行車輛限號出行政策，鼓勵民眾不開車低碳出行，某甲乙兩個單位各有200名員工，為了了解員工低碳出行的情況，統計了12月5日到12月14日共10天的低碳出行的人數，畫出莖葉圖如下：
（1）若甲單位數據的平均數是122，求
；
（2）現從如圖的數據中任取4天的數據（甲、乙兩單位中各取2天），記其中甲、乙兩單位員工低碳出行人數不低于130人的天數為
， 
，令
，求
的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
