
【題目】如圖,在寬為![]() 的路邊安裝路燈,燈柱
的路邊安裝路燈,燈柱![]() 高為
高為![]() ,燈桿
,燈桿![]() 是半徑為
是半徑為![]() 的圓
的圓![]() 的一段劣弧.路燈采用錐形燈罩,燈罩頂
的一段劣弧.路燈采用錐形燈罩,燈罩頂![]() 到路面的距離為
到路面的距離為![]() ,到燈柱所在直線的距離為
,到燈柱所在直線的距離為![]() .設
.設![]() 為燈罩軸線與路面的交點,圓心
為燈罩軸線與路面的交點,圓心![]() 在線段
在線段![]() 上.
上.

(1)當![]() 為何值時,點
為何值時,點![]() 恰好在路面中線上?
恰好在路面中線上?
(2)記圓心![]() 在路面上的射影為
在路面上的射影為![]() ,且
,且![]() 在線段
在線段![]() 上,求
上,求![]() 的最大值.
的最大值.
【答案】(1)當![]() 為
為![]() 時,點
時,點![]() 在路面中線上;(2)
在路面中線上;(2)![]()
【解析】
(1)以O為原點,以OA所在直線為y軸建立平面直角坐標系,求出PQ的方程,設C(a,b),根據CA=CP=r列方程組可得出a,b的值,從而求出r的值;
(2)用a表示出直線PQ的斜率,得出PQ的方程,求出Q的坐標,從而可得出|HQ|關于a的函數,根據a的范圍和基本不等式得出|HQ|的最大值.
(1)以O為原點,以OA所在直線為y軸建立平面直角坐標系,則A(0,8),P(2,10),Q(7,0),
∴直線PQ的方程為2x+y﹣14=0.設C(a,b),則 ,
,
兩式相減得:a+b﹣10=0,又2a+b﹣14=0,解得a=4,b=6,
∴![]() .∴當
.∴當![]() 時,點Q恰好在路面中線上.
時,點Q恰好在路面中線上.
(2)由(1)知a+b﹣10=0,
當a=2時,燈罩軸線所在直線方程為x=2,此時HQ=0.
當a≠2時,燈罩軸線所在方程為:y﹣10=![]() (x﹣2),
(x﹣2),
令y=0可得x=12﹣![]() ,即Q(12﹣
,即Q(12﹣![]() ,0),
,0),
∵H在線段OQ上,∴12﹣![]() ≥a,解得2≤a≤10.
≥a,解得2≤a≤10.
∴|HQ|=12﹣![]() ﹣a=12﹣(
﹣a=12﹣(![]() +a)≤12﹣
+a)≤12﹣![]() =12﹣
=12﹣![]() ,
,
當且僅當![]() =a即a=
=a即a=![]() 時取等號.∴|HQ|的最大值為(12﹣
時取等號.∴|HQ|的最大值為(12﹣![]() )m.
)m.



 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某大型工廠有![]() 臺大型機器,在
臺大型機器,在![]() 個月中,
個月中,![]() 臺機器至多出現
臺機器至多出現![]() 次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需
次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需![]() 名工人進行維修.每臺機器出現故障的概率為
名工人進行維修.每臺機器出現故障的概率為![]() .已知
.已知![]() 名工人每月只有維修
名工人每月只有維修![]() 臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得
臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得![]() 萬元的利潤,否則將虧損
萬元的利潤,否則將虧損![]() 萬元.該工廠每月需支付給每名維修工人
萬元.該工廠每月需支付給每名維修工人![]() 萬元的工資.
萬元的工資.
(1)若每臺機器在當月不出現故障或出現故障時有工人進行維修,則稱工廠能正常運行.若該廠只有![]() 名維修工人,求工廠每月能正常運行的概率;
名維修工人,求工廠每月能正常運行的概率;
(2)已知該廠現有![]() 名維修工人.
名維修工人.
(ⅰ)記該廠每月獲利為![]() 萬元,求
萬元,求![]() 的分布列與數學期望;
的分布列與數學期望;
(ⅱ)以工廠每月獲利的數學期望為決策依據,試問該廠是否應再招聘![]() 名維修工人?
名維修工人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一批產品需要進行質量檢驗,檢驗方案是:先從這批產品中任取4件作檢驗,這4件產品中優質品的件數記為![]() .如果
.如果![]() ,再從這批產品中任取4件作檢驗,若都為優質品,則這批產品通過檢驗;如果
,再從這批產品中任取4件作檢驗,若都為優質品,則這批產品通過檢驗;如果![]() ,再從這批產品中任取1件作檢驗,若為優質品,則這批產品通過檢驗;其他情況下,這批產品都不能通過檢驗.假設這批產品的優質品率為
,再從這批產品中任取1件作檢驗,若為優質品,則這批產品通過檢驗;其他情況下,這批產品都不能通過檢驗.假設這批產品的優質品率為![]() ,即取出的產品是優質品的概率都為
,即取出的產品是優質品的概率都為![]() ,且各件產品是否為優質品相互獨立.
,且各件產品是否為優質品相互獨立.
(1)求這批產品通過檢驗的概率;
(2)已知每件產品檢驗費用為100元,凡抽取的每件產品都需要檢驗,對這批產品作質量檢驗所需的費用記為![]() (單位:元),求
(單位:元),求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校隨機抽取部分學生調查其上學路上所需時間(單位:分鐘),并將所得數據制成頻率分布直方圖(如圖),若上學路上所需時間的范圍為![]() ,樣本數據分組為
,樣本數據分組為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方圖中a的值;
(2)如果上學路上所需時間不少于40分鐘的學生可申請在學校住宿,若招收學生1200人,請估計所招學生中有多少人可以申請住宿;
(3)求該校學生上學路上所需的平均時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在數列{an}中,設a1為首項,其前n項和為Sn,若對任意的正整數m,n都有不等式S2m+S2n<2Sm+n(m≠n)恒成立,且2S6<S3.
(1)設數列{an}為等差數列,且公差為d,求![]() 的取值范圍;
的取值范圍;
(2)設數列{an}為等比數列,且公比為q(q>0且q≠1),求a1![]() q的取值范圍.
q的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為![]() 的函數
的函數![]() ,若同時滿足下列條件:
,若同時滿足下列條件:
①![]() 在
在![]() 內單調遞增或單調遞減;
內單調遞增或單調遞減;
②存在區間![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ;
;
那么把![]() 叫閉函數.
叫閉函數.
(1)求閉函數![]() 符合條件②的區間
符合條件②的區間![]() ;
;
(2)判斷函數![]() 是否為閉函數?并說明理由;
是否為閉函數?并說明理由;
(3)若![]() 是閉函數,求實數
是閉函數,求實數![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列![]() 中,
中,![]() ,且對任意
,且對任意![]() ,
,![]() 成等差數列,其公差為
成等差數列,其公差為![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,證明
,證明![]() 成等比數列(
成等比數列(![]() );
);
(3)若對任意![]() ,
,![]() 成等比數列,其公比為
成等比數列,其公比為![]() ,設
,設![]() ,證明數列
,證明數列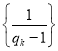 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓:![]() 的四個頂點圍成的四邊形的面積為
的四個頂點圍成的四邊形的面積為![]() ,原點到直線
,原點到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知定點![]() ,是否存在過
,是否存在過![]() 的直線
的直線![]() ,使
,使![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以
兩點,且以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 的左頂點?若存在,求出
的左頂點?若存在,求出![]() 的方程:若不存在,請說明理由.
的方程:若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com