
【題目】已知一家公司生產某種品牌服裝的年固定成本為10萬元,每生產1千件需另投入2.7萬元.設該公司一年內共生產該品牌服裝x千件并全部銷售完,每千件的銷售收入為![]() 萬元,且
萬元,且 .
.
(1)寫出年利潤W(萬元)關于年產量x(千件)的函數解析式;
(2)年產量為多少千件時,該公司在這一品牌服裝的生產中所獲得利潤最大?(注:年利潤=年銷售收入﹣年總成本)
【答案】(1) ;(2)當年產量為9千件時,該公司在這一品牌服裝的生產中所獲年利潤最大.
;(2)當年產量為9千件時,該公司在這一品牌服裝的生產中所獲年利潤最大.
【解析】試題分析:本題考查的知識點是分段函數及函數的最值,分段函數分段處理,這是研究分段函數圖象和性質最核心的理念,具體做法是:分段函數的定義域、值域是各段上x、y取值范圍的并集,分段函數的奇偶性、單調性要在各段上分別論證;分段函數的最大值,是各段上最大值中的最大者.第一問,由年利潤W=年產量x×每千件的銷售收入為R(x)﹣成本,又由 ,且年固定成本為10萬元,每生產1千件需另投入2.7萬元.我們易得年利潤W(萬元)關于年產量x(千件)的函數解析式;
,且年固定成本為10萬元,每生產1千件需另投入2.7萬元.我們易得年利潤W(萬元)關于年產量x(千件)的函數解析式;
第二問,由第一問的解析式,我們求出各段上的最大值,即利潤的最大值,然后根據分段函數的最大值是各段上最大值的最大者,即可得到結果.
試題解析:(1)當![]() 時,
時, ![]() ;
;
當![]() 時,
時, ![]() .
.
∴ .
.
(2)①當![]() 時,由
時,由![]() ,得
,得![]() ,
,
且當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,
,
∴當![]() 時,W取最大值,且
時,W取最大值,且![]() ,
,
②當![]() 時,
時, ![]() ,
,
當且僅當![]() ,
,
即![]() 時,
時, ![]() ,
,
故當![]() 時,W取最大值38.
時,W取最大值38.
綜合①②知當![]() 時,W取最大值38.6萬元,故當年產量為9千件時,該公司在這一品牌服裝的生產中所獲年利潤最大.
時,W取最大值38.6萬元,故當年產量為9千件時,該公司在這一品牌服裝的生產中所獲年利潤最大.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源: 題型:
【題目】某商店為了解氣溫對某產品銷售量的影響,隨機記錄了該商店![]() 月份中
月份中![]() 天的日銷售量
天的日銷售量![]() (單位:千克)與該地當日最低氣溫
(單位:千克)與該地當日最低氣溫![]() (單位:℃)的數據,如表所示:
(單位:℃)的數據,如表所示:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 與
與![]() 的回歸方程
的回歸方程![]() :
:
(2)判斷![]() 與
與![]() 之間是正相關還是負相關;若該地
之間是正相關還是負相關;若該地![]() 月份某天的最低氣溫為
月份某天的最低氣溫為![]() ,請用(1)中的回歸方程預測該商店當日的銷售量.
,請用(1)中的回歸方程預測該商店當日的銷售量.
參考公式: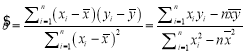 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】七巧板是古代中國勞動人民發明的一種中國傳統智力玩具,它由五塊等腰直角三角形,一塊正方形和一塊平行四邊形共七塊板組成.清陸以湉《冷廬雜識》卷一中寫道:近又有七巧圖,其式五,其數七,其變化之式多至千余.體物肖形,隨手變幻,蓋游戲之具,足以排悶破寂,故世俗皆喜為之.如圖是一個用七巧板拼成的正方形,若在此正方形中任取一點,則此點取自陰影部分的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1)是一直角墻角,![]() ,墻角的兩堵墻面和地面兩兩互相垂直.
,墻角的兩堵墻面和地面兩兩互相垂直.![]() 是一塊長
是一塊長![]() 為
為![]() 米,寬
米,寬![]() 為
為![]() 米的板材,現欲用板材與墻角圍成一個直棱柱空間堆放谷物.
米的板材,現欲用板材與墻角圍成一個直棱柱空間堆放谷物. 
(1)若按如圖(1)放置,如何放置板材才能使這個直棱柱空間最大?
(2)由于墻面使用受限,![]() 面只能使用
面只能使用![]() 米,
米,![]() 面只能使用
面只能使用![]() 米.此矩形板材可以折疊圍成一個直四棱柱空間,如圖(2),如何折疊板材才能使這個空間最大?
米.此矩形板材可以折疊圍成一個直四棱柱空間,如圖(2),如何折疊板材才能使這個空間最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
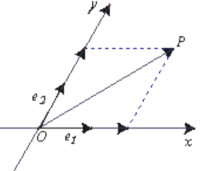
【題目】如圖,設![]() 是平面內相交成
是平面內相交成![]() 角的兩條數軸 ,
角的兩條數軸 ,![]() 分別是
分別是![]() 軸,
軸,![]() 軸正方向同向的單位向量,若向量
軸正方向同向的單位向量,若向量![]() ,則把有序數對
,則把有序數對![]() 叫做向量
叫做向量![]() 在坐標系
在坐標系![]() 中的坐標,假設
中的坐標,假設![]() .
.
(1)計算![]() 的大小;
的大小;
(2)設向量![]() ,若
,若![]() 與
與![]() 共線,求實數
共線,求實數![]() 的值;
的值;
(3)是否存在實數![]() ,使得
,使得![]() 與向量
與向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在請說明理由.
的值,若不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分12分)已知函數f(x)=ex, g(x)=lnx.
(1)設f(x)在x1處的切線為l1, g(x)在x2處的切線為l2,若l1//l2,求x1+g(x2)的值;
(2)若方程af 2(x)-f(x)-x=0有兩個實根,求實數a的取值范圍;
(3)設h(x)=f(x)(g(x)-b),若h(x)在[ln2,ln3]內單調遞減,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過
,過![]() 且垂直于
且垂直于![]() 軸的焦點弦的弦長為
軸的焦點弦的弦長為![]() ,過
,過![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() ,
,![]() 互相垂直,直線
互相垂直,直線![]() 過
過![]() 且與橢圓
且與橢圓![]() 交于點
交于點![]() ,
,![]() 兩點,直線
兩點,直線![]() 過
過![]() 且與橢圓
且與橢圓![]() 交于
交于![]() ,
,![]() 兩點.求
兩點.求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com