【題目】已知函數
.
（Ⅰ）討論函數
的單調性；
（Ⅱ）或
， 
時，證明： 
.
【答案】（I）詳見解析；（II）詳見解析.
【解析】試題分析：（Ⅰ）函數的導數
，分
和
兩種情況討論函數的單調性；（Ⅱ）設
，設
，再求
，分
和
兩種情況討論函數的單調性和函數的最小值，證明函數的最小值大于0.
試題解析：（Ⅰ） 
的定義域為
， 
，
當
時， 
， 
，函數
單調遞減；
當
時， 
， 
，函數
單調遞減， 
， 
，函數
單調遞增，
所以當
時，函數
在
單調遞減；
當
時，函數
在
單調遞減，在
單調遞增.
（Ⅱ）設
， 
，
設
， 
.
①當
時， 
， 
，所以
在
上單調遞增；
∴
，即
， 
在
上單調遞增，
∴
，不等式成立；
②當
時， 
， 
； 
， 
，
所以
在
上單調遞減，在
上單調遞增；
∴
，
即
， 
在
上單調遞增. ∴
，不等式成立；
綜上所述：當
， 
時，有
恒成立.
中考解讀考點精練系列答案
各地期末復習特訓卷系列答案
小博士期末闖關100分系列答案科目：高中數學 來源： 題型：
【題目】某大學為調研學生在
， 
兩家餐廳用餐的滿意度，從在
， 
兩家餐廳都用過餐的學生中隨機抽取了100人，每人分別對這兩家餐廳進行評分，滿分均為60分.
整理評分數據，將分數以10為組距分成6組： 
， 
， 
， 
， 
， 
，得到
餐廳分數的頻率分布直方圖，和
餐廳分數的頻數分布表：
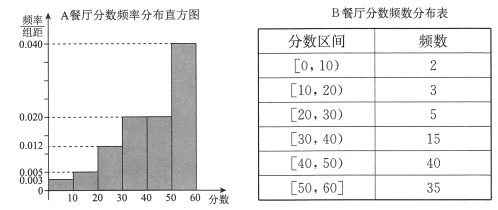
（Ⅰ）在抽樣的100人中，求對
餐廳評分低于30的人數；
（Ⅱ）從對
餐廳評分在
范圍內的人中隨機選出2人，求2人中恰有1人評分在
范圍內的概率；
（Ⅲ）如果從
， 
兩家餐廳中選擇一家用餐，你會選擇哪一家？說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，拋物線
的頂點是原點，以
軸為對稱軸，且經過點
.
（Ⅰ）求拋物線
的方程；
（Ⅱ）設點
， 
在拋物線
上，直線
， 
分別與
軸交于點
， 
， 
.求直線
的斜率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C所對邊分別為a，b，c且acosC，bcosB，ccosA成等差數列．
（1）求B的值；
（2）求2sin2A﹣1+cos（A﹣C）的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，以
為極點， 
軸的正半軸為極軸建立極坐標系．若直線
的極坐標方程為
，曲線
的極坐標方程為
，將曲線
上所有點的橫坐標縮短為原來的一半，縱坐標不變，然后再向右平移一個單位得到曲線
．
（Ⅰ）求曲線
的直角坐標方程；
（Ⅱ）已知直線
與曲線
交于
兩點，點
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司2016年前三個月的利潤（單位：百萬元）如下：
月份 | 1 | 2 | 3 |
利潤 | 2 | 3.9 | 5.5 |
（1）求利潤
關于月份
的線性回歸方程；
（2）試用（1）中求得的回歸方程預測4月和5月的利潤；
（3）試用（1）中求得的回歸方程預測該公司2016年從幾月份開始利潤超過1000萬？
相關公式：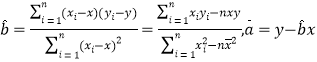
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國是世界上嚴重缺水的國家，某市政府為了鼓勵居民節約用水，計劃調整居民生活用水收費方案，擬確定一個合理的月用水量標準
（噸），一位居民的月用水量不超過
的部分按平價收費，超過
的部分按議價收費，為了了解居民用水情況，通過抽樣，獲得了某年100位居民每人的月均用水量（單位：噸），將數據按照
， 
，…， 
分成9組，制成了如圖所示的頻率分布直方圖.
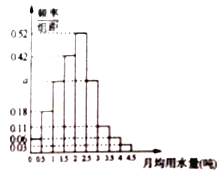
（1）求直方圖中
的值；
（2）若將頻率視為概率，從該城市居民中隨機抽取3人，記這3人中月均用水量不低于3噸的人數為
，求
的分布列與數學期望.
（3）若該市政府希望使85%的居民每月的用水量不超過標準
（噸），估計
的值（精確到0.01），并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
