
【題目】為了解甲、乙兩廠產(chǎn)品的質(zhì)量,從兩廠生產(chǎn)的產(chǎn)品中分別隨機抽取各10件樣品,測量產(chǎn)品中某種元素的含量(單位:毫克),如圖是測量數(shù)據(jù)的莖葉圖:
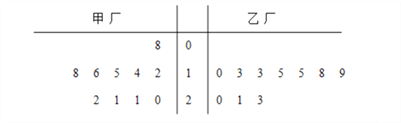
規(guī)定:當產(chǎn)品中的此種元素含量不小于16毫克時,該產(chǎn)品為優(yōu)等品.
(1)從乙廠抽出的上述10件樣品中,隨機抽取3件,求抽到的3件樣品中優(yōu)等品數(shù)![]() 的分布列及其數(shù)學期望
的分布列及其數(shù)學期望![]() ;
;
(2)從甲廠的10件樣品中有放回地逐個隨機抽取3件,也從乙廠的10件樣品中有放回地逐個隨機抽取3件,求抽到的優(yōu)等品數(shù)甲廠恰比乙廠多2件的概率.
【答案】(1)![]() ,分布列見解析(2)
,分布列見解析(2)![]()
【解析】試題分析:(1)![]() 的所有可能取值為
的所有可能取值為![]() ,由古典概型分別求概率,得到
,由古典概型分別求概率,得到![]() 的分布列,再求期望即可;(2)抽取的優(yōu)等品數(shù)甲廠比乙廠多兩件包括兩個基本事件:
的分布列,再求期望即可;(2)抽取的優(yōu)等品數(shù)甲廠比乙廠多兩件包括兩個基本事件:![]() “抽取的優(yōu)等品數(shù)甲廠
“抽取的優(yōu)等品數(shù)甲廠![]() 件,乙廠
件,乙廠![]() 件”,
件”,![]() “抽取的優(yōu)等品數(shù)甲廠
“抽取的優(yōu)等品數(shù)甲廠![]() 件,乙廠
件,乙廠![]() 件”,分別計算出它們的概率,再利用概率的加法公式得到抽取的優(yōu)等品數(shù)甲廠恰比乙廠多
件”,分別計算出它們的概率,再利用概率的加法公式得到抽取的優(yōu)等品數(shù)甲廠恰比乙廠多![]() 件的概率即可。
件的概率即可。
(1)由題意知,![]() 的值為0,1,2,3,
的值為0,1,2,3,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.
(2)甲廠抽取的樣本中優(yōu)等品有6件,優(yōu)等品率為![]() ,
,
乙廠抽取的樣本中有5件,優(yōu)等品率為![]() ,
,
抽取的優(yōu)等品數(shù)甲廠恰比乙廠多2件包括2個事件,
即![]() “抽取的優(yōu)等品數(shù)甲廠2件,乙廠0件”,
“抽取的優(yōu)等品數(shù)甲廠2件,乙廠0件”, ![]() “抽取的優(yōu)等品數(shù)甲廠3件,乙廠1件”,
“抽取的優(yōu)等品數(shù)甲廠3件,乙廠1件”,
![]() ,
,
![]() ,
,
∴抽到的優(yōu)等品數(shù)甲廠恰比乙廠多2件的概率:![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,拋物線上橫坐標為
,拋物線上橫坐標為![]() 的點到拋物線頂點的距離與該點到拋物線準線的距離相等。
的點到拋物線頂點的距離與該點到拋物線準線的距離相等。
(1)求拋物線![]() 的方程;
的方程;
(2)設(shè)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,若
兩點,若![]() ,求實數(shù)
,求實數(shù)![]() 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,兩條公路AP與AQ夾角A為鈍角,其正弦值是![]()
![]() .甲乙兩人從A點出發(fā)沿著兩條公路進行搜救工作,甲沿著公路AP方向,乙沿著公路AQ方向.
.甲乙兩人從A點出發(fā)沿著兩條公路進行搜救工作,甲沿著公路AP方向,乙沿著公路AQ方向.

(1)當甲前進5km的時候到達P處,同時乙到達Q處,通訊測得甲乙兩人相距![]()
![]() km,求乙在此時前進的距離AQ;
km,求乙在此時前進的距離AQ;
(2)甲在5公里處原地未動,乙回頭往A方向行走至M點收到甲發(fā)出的信號,此時M點看P、Q兩點的張角為![]() (張角為
(張角為![]() QMP)
QMP)![]() ,求甲乙兩人相距的距離MP的長.
,求甲乙兩人相距的距離MP的長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校對高一年級學生寒假參加社區(qū)服務(wù)的次數(shù)進行了統(tǒng)計,隨機抽取了![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區(qū)服務(wù)的次數(shù),根據(jù)此數(shù)據(jù)作出了頻率分布統(tǒng)計表和頻率分布直方圖如下:
名學生參加社區(qū)服務(wù)的次數(shù),根據(jù)此數(shù)據(jù)作出了頻率分布統(tǒng)計表和頻率分布直方圖如下:

(1)求表中![]() 的值和頻率分布直方圖中
的值和頻率分布直方圖中![]() 的值,并根據(jù)頻率分布直方圖估計該校高一學生寒假參加社區(qū)服務(wù)次數(shù)的中位數(shù);
的值,并根據(jù)頻率分布直方圖估計該校高一學生寒假參加社區(qū)服務(wù)次數(shù)的中位數(shù);
(2)如果用分層抽樣的方法從樣本服務(wù)次數(shù)在![]() 和
和![]() 的人中共抽取6人,再從這6人中選2人,求2人服務(wù)次數(shù)都在
的人中共抽取6人,再從這6人中選2人,求2人服務(wù)次數(shù)都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知A(4, 0),B(2, 2),C (6, 0),記△ABC的外接圓為⊙P.
(1)求⊙P的方程.
(2)對于線段PA上的任意一點G,是否存在以B為圓心的圓,在圓B上總能找到不同的兩點E、F,滿足![]() =
=![]() ,若存在,求圓B的半徑
,若存在,求圓B的半徑![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某研究性學習小組對春季晝夜溫差大小與某花卉種子發(fā)芽多少之間的關(guān)系進行研究,他們分別記錄了3月1日至3月5日的每天晝夜溫差![]() 與實驗室每天每100顆種子浸泡后的發(fā)芽數(shù)
與實驗室每天每100顆種子浸泡后的發(fā)芽數(shù)![]() ,作了初步處理,得到下表:
,作了初步處理,得到下表:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
溫差 | 10 | 11 | 13 | 12 | 9 |
發(fā)芽率 | 23 | 25 | 30 | 26 | 16 |
(1)從3月1日至3月5日中任選2天,記發(fā)芽的種子數(shù)分別為![]() ,求事件“
,求事件“![]() 均小于26”的概率;
均小于26”的概率;
(2)請根據(jù)3月1日至3月5日的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,并預報3月份晝夜溫差為14度時實驗室每天100顆種子浸泡后的發(fā)芽(取整數(shù)值).
,并預報3月份晝夜溫差為14度時實驗室每天100顆種子浸泡后的發(fā)芽(取整數(shù)值).
附:回歸方程![]() 中的斜率和截距最小二乘法估計公式分別為:
中的斜率和截距最小二乘法估計公式分別為: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,又
,又![]() 平面
平面![]() ,且
,且![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() .
.
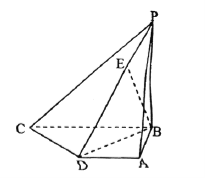
(1)求異面直線![]() 與
與![]() 所成的角的大小;
所成的角的大小;
(2)求證:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() ,關(guān)于
,關(guān)于![]() 的方程
的方程![]() 有三個不同的實根,求
有三個不同的實根,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com