
【題目】已知橢圓![]() :
: ![]() ,設直線
,設直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() ,且
,且![]() .若點
.若點![]() 滿足
滿足![]() ,則
,則![]() =______________.
=______________.
【答案】![]() 或
或![]()
【解析】由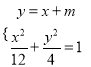 ,得
,得![]() ①
①
∵直線l與橢圓C交于不同兩點![]() ,
,
∴![]() 得
得![]() <16.
<16.
設![]() 則
則![]() ,
,![]() 是方程①的兩根,
是方程①的兩根,
則![]() .
.
∴![]() .
.
又由![]() ,得
,得![]() ,解之m=±2.
,解之m=±2.
據題意知,點P為線段AB的中垂線與直線y=2的交點。
設AB的中點為![]() ,則
,則![]() ,
,
當m=2時, ![]() .
.
∴此時,線段AB的中垂線方程為![]() ,即y=x1.
,即y=x1.
令y=2,得![]() =3.
=3.
當m=2時,E(![]() ,
,![]() ).
).
∴此時,線段AB的中垂線方程為![]() ,即y=x+1.
,即y=x+1.
令y=2,得![]() =1.
=1.
綜上所述, ![]() 的值為3或1.
的值為3或1.
點睛: 本題主要考查直線與圓錐曲線位置關系,所使用方法為韋達定理法:因直線的方程是一次的,圓錐曲線的方程是二次的,故直線與圓錐曲線的問題常轉化為方程組關系問題,最終轉化為一元二次方程問題,故用韋達定理及判別式是解決圓錐曲線問題的重點方法之一,尤其是弦中點問題,弦長問題,可用韋達定理直接解決,但應注意不要忽視判別式的作用.


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:高中數學 來源: 題型:
【題目】已知A={x|(2x)2﹣62x+8≤0},函數f(x)=log2x(x∈A).
(1)求函數f(x)的定義域;
(2)若函數h(x)=[f(x)]2﹣log2(2x),求函數h(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|﹣1≤x≤10},集合B={x|2x﹣6≥0}.
求R(A∪B);
已知C={x|a<x<a+1},且CA,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知橢圓![]() 的焦距為
的焦距為 ![]() ,直線
,直線![]() 被橢圓
被橢圓 ![]() 截得的弦長為
截得的弦長為![]() .
.

(1)求橢圓 ![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓 ![]() 上的動點,過原點
上的動點,過原點![]() 引兩條射線
引兩條射線![]() 與圓
與圓![]() 分別相切,且
分別相切,且![]() 的斜率
的斜率![]() 存在. ①試問
存在. ①試問 ![]() 是否為定值?若是,求出該定值,若不是,說明理由;
是否為定值?若是,求出該定值,若不是,說明理由;
②若射線![]() 與橢圓
與橢圓 ![]() 分別交于點
分別交于點![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,點 ![]() 的極坐標是
的極坐標是![]() ,曲線
,曲線 ![]() 的極坐標方程為
的極坐標方程為![]() .以極點為坐標原點,極軸為
.以極點為坐標原點,極軸為 ![]() 軸的正半軸建立平面直角坐標系,斜率為
軸的正半軸建立平面直角坐標系,斜率為 ![]() 的直線
的直線 ![]() 經過點
經過點![]() .
.
(1)寫出直線 ![]() 的參數方程和曲線
的參數方程和曲線 ![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線 ![]() 和曲線
和曲線![]() 相交于兩點
相交于兩點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】孝感星河天街購物廣場某營銷部門隨機抽查了100名市民在2017年國慶長假期間購物廣場的消費金額,所得數據如表,已知消費金額不超過3千元與超過3千元的人數比恰為3:2.

(1)試確定![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值,并補全頻率分布直方圖(如圖);
的值,并補全頻率分布直方圖(如圖);
(2)用分層抽樣的方法從消費金額在![]() 、
、![]() 和
和![]() 的三個群體中抽取7人進行問卷調查,則各小組應抽取幾人?若從這7人中隨機選取2人,則此2人來自同一群體的概率是多少?
的三個群體中抽取7人進行問卷調查,則各小組應抽取幾人?若從這7人中隨機選取2人,則此2人來自同一群體的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com