
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100].
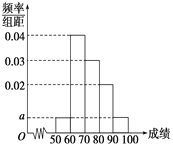
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示,求數學成績在[50,90)之外的人數.
分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
【答案】(1)![]() (2)
(2)![]() (分)(3)
(分)(3)![]()
【解析】
(1)由頻率分布直方圖的性質列方程即可得到![]() 的值;
的值;
(2)由平均數加權公式可得平均數,計算出結果即可;
(3)按表中所給的數據分別計算出數學成績在分數段的人數,從總人數中減去這些段內的人數即可得出數學成績在![]() 之外的人數.
之外的人數.
解(1)由頻率分布直方圖知(2a+0.02+0.03+0.04)×10=1,解得a=0.005.
(2)由頻率分布直方圖知這100名學生語文成績的平均分為55×0.005×10+65×0.04×10+75×0.03×10+85×0.02×10+95×0.005×10=73(分).
(3)由頻率分布直方圖知語文成績在[50,60),[60,70),[70,80),[80,90)各分數段的人數依次為
0.005×10×100=5,0.04×10×100=40,0.03×10×100=30,0.02×10×100=20.
由題中給出的比例關系知數學成績在上述各分數段的人數依次為
![]() .
.
故數學成績在[50,90)之外的人數為100-(5+20+40+25)=10.


科目:高中數學 來源: 題型:
【題目】為了解某班學生喜好體育運動是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
喜好體育運動 | 不喜好體育運動 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 | 50 |
已知按喜好體育運動與否,采用分層抽樣法抽取容量為10的樣本,則抽到喜好體育運動的人數為6.
(1)請將上面的列聯表補充完整;
(2)能否在犯錯概率不超過0.01的前提下認為喜好體育運動與性別有關?說明理由.
附:![]()
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱ABCDA1B1C1D1中,側棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=![]() ,且點M和N分別為B1C和D1D的中點.
,且點M和N分別為B1C和D1D的中點.

(Ⅰ)求證:MN∥平面ABCD;
(Ⅱ)求二面角D1-AC-B1的正弦值;
(Ⅲ)設E為棱A1B1上的點.若直線NE和平面ABCD所成角的正弦值為![]() ,求線段A1E的長.
,求線段A1E的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有一組圓![]() :
:![]() .下列四個命題其中真命題的序號是____
.下列四個命題其中真命題的序號是____
①存在一條定直線與所有的圓均相切;
②存在一條定直線與所有的圓均相交;
③存在一條定直線與所有的圓均不相交;
④所有的圓均不經過原點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其圖像相鄰的兩個對稱中心之間的距離為
,其圖像相鄰的兩個對稱中心之間的距離為![]() ,且有一條對稱軸為直線
,且有一條對稱軸為直線![]() ,則下列判斷正確的是 ( )
,則下列判斷正確的是 ( )
A. 函數![]() 的最小正周期為
的最小正周期為![]()
B. 函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱
對稱
C. 函數![]() 在區間
在區間![]() 上單調遞增
上單調遞增
D. 函數![]() 的圖像關于點
的圖像關于點![]() 對稱
對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以點![]() 為圓心的圓C被直線
為圓心的圓C被直線![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求圓C的標準方程:
(2)求過![]() 與圓C相切的直線方程:
與圓C相切的直線方程:
(3)若Q是直線![]() 上的動點,QR,QS分別切圓C于R,S兩點.試問:直線RS是否恒過定點?若是,求出恒過點坐標:若不是,說明理由.
上的動點,QR,QS分別切圓C于R,S兩點.試問:直線RS是否恒過定點?若是,求出恒過點坐標:若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其圖象與
,其圖象與![]() 軸相鄰的兩個交點的距離為
軸相鄰的兩個交點的距離為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若將![]() 的圖象向左平移
的圖象向左平移![]() 個長度單位得到函數
個長度單位得到函數![]() 的圖象恰好經過點
的圖象恰好經過點![]() ,求當
,求當![]() 取得最小值時,
取得最小值時,![]() 在
在![]() 上的單調區間.
上的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓x2+y2=8內有一點P0(-1,2),AB為過點P0且傾斜角為α的弦.
(1)當α=![]() 時,求AB的長;
時,求AB的長;
(2)當弦AB被點P0平分時,寫出直線AB的方程(用直線方程的一般式表示).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com