
【題目】已知點F是拋物線![]() 的焦點,若點
的焦點,若點![]() 在拋物線C上,且
在拋物線C上,且![]()
(1)求拋物線C的方程;
(2)動直線![]() 與拋物線C相交于
與拋物線C相交于![]() 兩點,問:在x軸上是否存在定點
兩點,問:在x軸上是否存在定點![]() (其中
(其中![]() ),使得x軸平分
),使得x軸平分![]() ?若存在,求出點D的坐標;若不存在,請說明理由.
?若存在,求出點D的坐標;若不存在,請說明理由.
科目:高中數學 來源: 題型:
【題目】“團購”已經滲透到我們每個人的生活,這離不開快遞行業的發展,下表是2013-2017年全國快遞業務量(x億件:精確到0.1)及其增長速度(y%)的數據
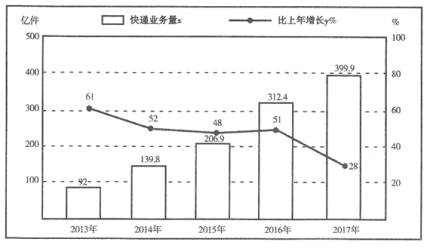
(1)試計算2012年的快遞業務量;
(2)分別將2013年,2014年,…,2017年記成年的序號t:1,2,3,4,5;現已知y與t具有線性相關關系,試建立y關于t的回歸直線方程![]() ;
;
(3)根據(2)問中所建立的回歸直線方程,估算2019年的快遞業務量
附:回歸直線的斜率和截距地最小二乘法估計公式分別為: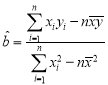 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著網絡營銷和電子商務的興起,人們的購物方式更具多樣化,某調查機構隨機抽取10名購物者進行采訪,5名男性購物者中有3名傾向于選擇網購,2名傾向于選擇實體店,5名女性購物者中有2名傾向于選擇網購,3名傾向于選擇實體店.
(1)若從10名購物者中隨機抽取2名,其中男、女各一名,求至少1名傾向于選擇實體店的概率;
(2)若從這10名購物者中隨機抽取3名,設X表示抽到傾向于選擇網購的男性購物者的人數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著現代電子技術的迅猛發展,關于元件和系統可靠性的研究已發展成為一門新的學科——可靠性理論.在可靠性理論中,一個元件正常工作的概率稱為該元件的可靠性.元件組成系統,系統正常工作的概率稱為該系統的可靠性.現有![]() (
(![]() ,
,![]() )種電子元件,每種2個,每個元件的可靠性均為
)種電子元件,每種2個,每個元件的可靠性均為![]() (
(![]() ).當某元件不能正常工作時,該元件在電路中將形成斷路.現要用這
).當某元件不能正常工作時,該元件在電路中將形成斷路.現要用這![]() 個元件組成一個電路系統,有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態時,系統正常工作.
個元件組成一個電路系統,有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態時,系統正常工作.
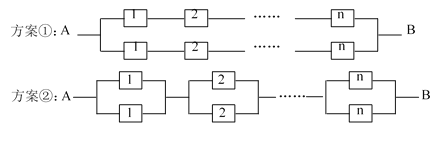
(1)(i)分別寫出按方案①和方案②建立的電路系統的可靠性![]() 、
、![]() (用
(用![]() 和
和![]() 表示);
表示);
(ii)比較![]() 與
與![]() 的大小,說明哪種連接方案更穩定可靠;
的大小,說明哪種連接方案更穩定可靠;
(2)設![]() ,
,![]() ,已知按方案②建立的電路系統可以正常工作,記此時系統中損壞的元件個數為
,已知按方案②建立的電路系統可以正常工作,記此時系統中損壞的元件個數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與函數
與函數![]() (
(![]() )的圖象相交,將其中三個相鄰交點從左到右依次記為A,B,C,且滿足
)的圖象相交,將其中三個相鄰交點從左到右依次記為A,B,C,且滿足![]()
![]() 有下列結論:
有下列結論:
①n的值可能為2
②當![]() ,且
,且![]() 時,
時,![]() 的圖象可能關于直線
的圖象可能關于直線![]() 對稱
對稱
③當![]() 時,有且僅有一個實數ω,使得
時,有且僅有一個實數ω,使得![]() 在
在![]() 上單調遞增;
上單調遞增;
④不等式![]() 恒成立
恒成立
其中所有正確結論的編號為( )
A.③B.①②C.②④D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《山東省高考改革試點方案》規定:從2017年秋季高中入學的新生開始,不分文理科;2020年開始,高考總成績由語數外3門統考科目和物理、化學等六門選考科目構成.將每門選考科目的考生原始成績從高到低劃分為A、B+、B、C+、C、D+、D、E共8個等級.參照正態分布原則,確定各等級人數所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%.選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八個分數區間,得到考生的等級成績.
某校高一年級共2000人,為給高一學生合理選科提供依據,對六個選考科目進行測試,其中物理考試原始成績基本服從正態分布N(60,169).
(Ⅰ)求物理原始成績在區間(47,86)的人數;
(Ⅱ)按高考改革方案,若從全省考生中隨機抽取3人,記X表示這3人中等級成績在區間[61,80]的人數,求X的分布列和數學期望.
(附:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com