
【題目】已知函數![]() .
.
(1)若![]() ,求
,求![]() 的零點個數;
的零點個數;
(2)若![]() ,
,![]() ,證明:
,證明:![]() ,
,![]() .
.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】
(1)將a的值代入f(x),再求導得![]() ,在定義域內討論函數單調性,再由函數的最小值正負來判斷它的零點個數;(2)把a的值代入f(x),將
,在定義域內討論函數單調性,再由函數的最小值正負來判斷它的零點個數;(2)把a的值代入f(x),將![]() 整理化簡為
整理化簡為![]() ,即證明該不等式在
,即證明該不等式在![]() 上恒成立,構造新的函數
上恒成立,構造新的函數![]() ,利用導數可知其在定義域上的最小值,構造函數
,利用導數可知其在定義域上的最小值,構造函數![]() ,由導數可知其定義域上的最大值,二者比較大小,即得證。
,由導數可知其定義域上的最大值,二者比較大小,即得證。
(1)解:因為![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
而![]() ,
,![]() ,
,![]() ,
,
所以![]() 的零點個數為1.
的零點個數為1.
(2)證明:因為![]() ,從而
,從而![]() .
.
又因為![]() ,
,
所以要證![]() ,
,![]() 恒成立,
恒成立,
即證![]() ,
,![]() 恒成立,
恒成立,
即證![]() ,
,![]() 恒成立.
恒成立.
設![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() ,
,![]() 單調遞減.
單調遞減.
所以![]() .
.
設![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() ,
,![]() 單調遞減.
單調遞減.
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() 恒成立,
恒成立,
即![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】華中師大附中中科教處為了研究高一學生對物理和數學的學習是否與性別有關,從高一年級抽取60,名同學(男同學30名,女同學30名),給所有同學物理題和數學題各一題,讓每位同學自由選擇一道題進行解答.選題情況如下表:(單位:人)

(1)在犯錯誤的概率不超過1%是條件下,能否判斷高一學生對物理和數學的學習與性別有關?
(2)經過多次測試后發現,甲每次解答一道物理題所用的時間5—8分鐘,乙每次解答一道物理題所用的時間為6—8分鐘,現甲、乙解同一道物理題,求甲比乙先解答完的概率;
(3)現從選擇做物理題的8名女生中任意選取兩人,對題目的解答情況進行全程研究,記甲、乙兩女生被抽到的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
已知函數![]() 的圖象在
的圖象在![]() 上連續不斷,定義:
上連續不斷,定義:
![]()
![]() ,
,
![]()
![]() .
.
其中,![]() 表示函數
表示函數![]() 在
在![]() 上的最小值,
上的最小值,![]() 表示函數
表示函數![]() 在
在![]() 上的最大值.若存在最小正整數
上的最大值.若存在最小正整數![]() ,使得
,使得![]() 對任意的
對任意的![]() 成立,則稱函數
成立,則稱函數![]() 為
為![]() 上的“
上的“![]() 階收縮函數”.
階收縮函數”.
(Ⅰ)若![]() ,
,![]() ,試寫出
,試寫出![]() ,
,![]() 的表達式;
的表達式;
(Ⅱ)已知函數![]() ,
,![]() ,試判斷
,試判斷![]() 是否為
是否為![]() 上的“
上的“![]() 階收縮函數”,如果是,求出對應的
階收縮函數”,如果是,求出對應的![]() ;如果不是,請說明理由;
;如果不是,請說明理由;
(Ⅲ)已知![]() ,函數
,函數![]() 是
是![]() 上的2階收縮函數,求
上的2階收縮函數,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,分別過橢圓![]() 左、右焦點
左、右焦點![]() 的動直線
的動直線![]() 相交于
相交于![]() 點,與橢圓
點,與橢圓![]() 分別交于
分別交于![]() 與
與![]() 不同四點,直線
不同四點,直線![]() 的斜率
的斜率![]() 滿足
滿足![]() , 已知
, 已知![]() 與
與![]() 軸重合時,
軸重合時, ![]() .
.
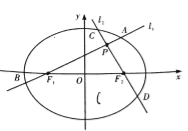
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在定點![]() 使得
使得![]() 為定值,若存在,求出
為定值,若存在,求出![]() 點坐標并求出此定值,若不存在,
點坐標并求出此定值,若不存在,
說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的極值;
的極值;
(Ⅱ)若函數![]() 的兩個零點為
的兩個零點為![]() ,記
,記![]() ,證明:
,證明:![]() .
.
【答案】(Ⅰ)極大值為![]() ,無極小值;(Ⅱ)證明見解析.
,無極小值;(Ⅱ)證明見解析.
【解析】分析:(Ⅰ)先判斷函數![]() 在
在![]() 上的單調性,然后可得當
上的單調性,然后可得當![]() 時,
時,![]() 有極大值,無極小值.(Ⅱ)不妨設
有極大值,無極小值.(Ⅱ)不妨設![]() ,由題意可得
,由題意可得![]() ,即
,即![]() ,又由條件得
,又由條件得![]() ,構造
,構造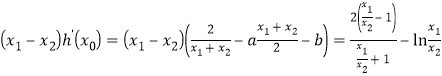 ,令
,令![]() ,則
,則![]() ,利用導數可得
,利用導數可得![]() ,故得
,故得![]() ,又
,又![]() ,所以
,所以![]() .
.
詳解:(Ⅰ)![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
且當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞減,
上單調遞減,
∴當![]() 時,
時,![]() 有極大值,且
有極大值,且![]() ,無極小值.
,無極小值.
(Ⅱ)![]() 函數
函數![]() 的兩個零點為
的兩個零點為![]() ,不妨設
,不妨設![]() ,
,
![]() ,
,![]() .
.
![]()
![]() ,
,
即![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,

![]()
![]()
 .
.
令![]() ,則
,則![]()
![]() ,
,
![]() 在
在![]() 上單調遞減,
上單調遞減,
故![]() ,
,
 ,
,
即![]() ,
,
又![]() ,
,
![]() .
.
點睛:(1)研究方程根的情況,可以通過導數研究函數的單調性、最大(小)值、函數的變化趨勢等,根據題目要求,畫出函數圖象的大體圖象,然后通過數形結合的思想去分析問題,可以使得問題的求解有一個清晰、直觀的整體展現.
(2)證明不等式時常采取構造函數的方法,然后通過判斷函數的單調性,借助函數的最值進行證明.
【題型】解答題
【結束】
22
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ).以坐標原點
).以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,已知曲線
軸正半軸為極軸,建立極坐標系,已知曲線![]() 的極坐標方程為:
的極坐標方程為:![]() .
.
(Ⅰ)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】互聯網正在改變著人們的生活方式,在日常消費中手機支付正逐漸取代現金支付成為人們首選的支付方式. 某學生在暑期社會活動中針對人們生活中的支付方式進行了調查研究. 采用調查問卷的方式對100名18歲以上的成年人進行了研究,發現共有60人以手機支付作為自己的首選支付方式,在這60人中,45歲以下的占![]() ,在仍以現金作為首選支付方式的人中,45歲及以上的有30人.
,在仍以現金作為首選支付方式的人中,45歲及以上的有30人.
(1)從以現金作為首選支付方式的40人中,任意選取3人,求這3人至少有1人的年齡低于45歲的概率;
(2)某商家為了鼓勵人們使用手機支付,做出以下促銷活動:凡是用手機支付的消費者,商品一律打八折. 已知某商品原價50元,以上述調查的支付方式的頻率作為消費者購買該商品的支付方式的概率,設銷售每件商品的消費者的支付方式都是相互獨立的,求銷售10件該商品的銷售額的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 為自然對數的底數,
為自然對數的底數, ![]() ……).
……).
(1)令![]() ,若
,若![]() 對任意的
對任意的![]() 恒成立,求實數
恒成立,求實數![]() 的值;
的值;
(2)在(1)的條件下,設![]() 為整數,且對于任意正整數
為整數,且對于任意正整數![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知10件不同產品中有3件是次品,現對它們一一取出(不放回)進行檢測,直至取出所有次品為止.
(1)若恰在第5次取到第一件次品,第10次才取到最后一件次品,則這樣的不同測試方法數有多少?
(2)若恰在第6次取到最后一件次品,則這樣的不同測試方法數是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com