
【題目】某公司生產一批![]() 產品需要原材料500噸,每噸原材料可創造利潤12萬元,該公司通過設備升級,生產這批
產品需要原材料500噸,每噸原材料可創造利潤12萬元,該公司通過設備升級,生產這批![]() 產品所需原材料減少了
產品所需原材料減少了![]() 噸,且每噸原材料創造的利潤提高了
噸,且每噸原材料創造的利潤提高了![]() ;若將少用的
;若將少用的![]() 噸原材料全部用于生產公司新開發的
噸原材料全部用于生產公司新開發的![]() 產品,每噸原材料創造的利潤為
產品,每噸原材料創造的利潤為![]() 萬元,其中a>0.
萬元,其中a>0.
(1)若設備升級后生產這批A產品的利潤不低于原來生產該批A產品的利潤,求![]() 的取值范圍;
的取值范圍;
(2)若生產這批B產品的利潤始終不高于設備升級后生產這批A產品的利潤,求![]() 的最大值.
的最大值.
 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】如圖1,在高為2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,過
,過![]() 、
、![]() 分別作
分別作![]() ,
, ![]() ,垂足分別為
,垂足分別為![]() 、
、![]() 。已知
。已知![]() ,將梯形
,將梯形![]() 沿
沿![]() 、
、![]() 同側折起,得空間幾何體
同側折起,得空間幾何體![]() ,如圖2。
,如圖2。
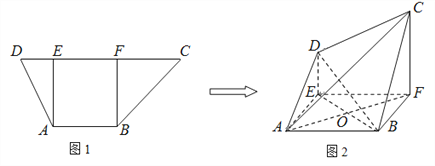
(1)若![]() ,證明:
,證明: ![]() ;
;
(2)若![]() ,證明:
,證明: ![]() ;
;
(3)在(1),(2)的條件下,求三棱錐![]() 的體積。
的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的空間幾何體中,平面![]() 平面
平面![]() ,
,![]() 與
與![]() 都是邊長為2的等邊三角形,
都是邊長為2的等邊三角形,![]() ,
,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,且點E在平面
,且點E在平面![]() 上的射影落在
上的射影落在![]() 的平分線上.
的平分線上.
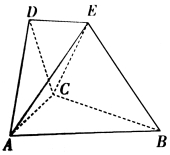
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的圖象在點
)的圖象在點![]() 處的切線的斜率為
處的切線的斜率為![]() ,且函數
,且函數![]() 為偶函數.若函數
為偶函數.若函數![]() 滿足下列條件:①
滿足下列條件:①![]() ;②對一切實數
;②對一切實數![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)求函數![]() 的表達式;
的表達式;
(2)設函數![]() (
(![]() )的兩個極值點
)的兩個極值點![]() ,
,![]() (
(![]() )恰為
)恰為![]() 的零點.當
的零點.當![]() 時,求
時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 為
為![]() 上異于原點的任意一點,過點
上異于原點的任意一點,過點![]() 的直線
的直線![]() 交
交![]() 于另一點
于另一點![]() ,交
,交![]() 軸的正半軸于點
軸的正半軸于點![]() ,且有
,且有![]() .當點
.當點![]() 的橫坐標為3時,
的橫坐標為3時,![]() 為正三角形.
為正三角形.
(1)求![]() 的方程;
的方程;
(2)延長![]() 交拋物線于點
交拋物線于點![]() ,過點
,過點![]() 作拋物線的切線
作拋物線的切線![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com