
【題目】已知定義域為![]() 的函數
的函數![]() 是奇函數.
是奇函數.
(1)求![]() 的解析式;
的解析式;
(2)試判斷![]() 的單調性,并用定義法證明;
的單調性,并用定義法證明;
(3)若存在![]() ,使得不等式
,使得不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】
已知拋物線![]() ,過點
,過點![]() 的直線
的直線![]() 與拋物線交于
與拋物線交于![]() 、
、![]() 兩點,且直線
兩點,且直線![]() 與
與![]() 軸交于點
軸交于點![]() .(1)求證:
.(1)求證:![]() ,
,![]() ,
,![]() 成等比數列;
成等比數列;
(2)設![]() ,
,![]() ,試問
,試問![]() 是否為定值,若是,求出此定值;若不是,請說明理由.
是否為定值,若是,求出此定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖半圓![]() 的直徑為4,
的直徑為4,![]() 為直徑
為直徑![]() 延長線上一點,且
延長線上一點,且![]() ,
,![]() 為半圓周上任一點,以
為半圓周上任一點,以![]() 為邊作等邊
為邊作等邊![]() (
(![]() 、
、![]() 、
、![]() 按順時針方向排列)
按順時針方向排列)
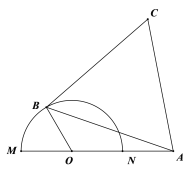
(1)若等邊![]() 邊長為
邊長為![]() ,
,![]() ,試寫出
,試寫出![]() 關于
關于![]() 的函數關系;
的函數關系;
(2)問![]() 為多少時,四邊形
為多少時,四邊形![]() 的面積最大?這個最大面積為多少?
的面積最大?這個最大面積為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在空間中,過點A作平面π的垂線,垂足為B,記B=fπ(A).設α,β是兩個不同的平面,對空間任意一點P,Q1=fβ[fα(P)],Q2=fα[fβ(P)],恒有PQ1=PQ2,則( )
A.平面α與平面β垂直
B.平面α與平面β所成的(銳)二面角為45°
C.平面α與平面β平行
D.平面α與平面β所成的(銳)二面角為60°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義域為
是定義域為![]() 的奇函數,當
的奇函數,當![]() .
.
(Ⅰ)求出函數![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答題卷上畫出函數![]() 的圖象,并根據圖象寫出
的圖象,并根據圖象寫出![]() 的單調區間;
的單調區間;

(Ⅲ)若關于![]() 的方程
的方程![]() 有三個不同的解,求
有三個不同的解,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產A種型號的電腦.2013年平均每臺電腦的生產成本為5000元,并按純利潤為20%定出廠價,2014年開始,公司更新設備,加強管理,逐步推行股份制,從而使生產成本逐年降低,2017年平均每臺A種型號的電腦出廠價僅是2013年的80%,實現了純利潤50%.
(1)求2017年每臺A種型號電腦的生產成本;
(2)以2013年的生產成本為基數,用二分法求2013-2017年間平均每年生產成本降低的百分率(精確度001).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中常數
,其中常數![]() .
.
(1)令![]() ,將函數
,將函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位,再向上平移1個單位,得到函數
個單位,再向上平移1個單位,得到函數![]() ,求函數
,求函數![]() 的解析式;
的解析式;
(2)若![]() 在
在![]() 上單調遞增,求
上單調遞增,求![]() 的取值范圍;
的取值范圍;
(3)在(1)的條件下的函數![]() 的圖像,區間
的圖像,區間![]()
![]() 且
且![]() 滿足:
滿足:![]() 在
在![]() 上至少含有30個零點,在所有滿足上述條件的
上至少含有30個零點,在所有滿足上述條件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com