
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,橢圓的左,右焦點分別為F1,F2,點M為橢圓上的一個動點,△MF1F2面積的最大值為
,橢圓的左,右焦點分別為F1,F2,點M為橢圓上的一個動點,△MF1F2面積的最大值為![]() ,過橢圓外一點(m,0)(m>a)且傾斜角為
,過橢圓外一點(m,0)(m>a)且傾斜角為![]() 的直線l交橢圓于C,D兩點.
的直線l交橢圓于C,D兩點.
(1)求橢圓的方程;
(2)若![]() ,求m的值.
,求m的值.
【答案】(1)![]() ;(2)3.
;(2)3.
【解析】
(1)根據離心率和面積聯立方程解得橢圓方程.
(2)設直線方程為y![]() (x﹣m),聯立方程根據韋達定理得到x1+x2=m,x1x2
(x﹣m),聯立方程根據韋達定理得到x1+x2=m,x1x2![]() ,根據
,根據![]() 得到(x1﹣2,y1)(x2﹣2,y2)=0,代入化簡得到答案.
得到(x1﹣2,y1)(x2﹣2,y2)=0,代入化簡得到答案.
(1)∵離心率為![]() ,△MF1F2面積的最大值為
,△MF1F2面積的最大值為![]() ,
,
∴![]() ,①
,①![]() ,即bc=2
,即bc=2![]() ,②又∵b2=a2﹣c2,③
,②又∵b2=a2﹣c2,③
由①②③解得,a![]() ,b
,b![]() ,c=2,∴橢圓方程為
,c=2,∴橢圓方程為![]() .
.
(2)根據題意設直線l方程y﹣0=tan![]() (x﹣m),即y
(x﹣m),即y![]() (x﹣m),
(x﹣m),
C(x1,y1),D(x2,y2),
聯立直線l與橢圓的方程得2x2﹣2mx+m2﹣6=0,
∴x1+x2=m,x1x2![]() ,
,
y1y2![]() ,
,
若![]() ,則(x1﹣2,y1)(x2﹣2,y2)=0,
,則(x1﹣2,y1)(x2﹣2,y2)=0,
∴x1x2﹣2(x1+x2)+4+y1y2=0,∴![]() ,解得m=3.
,解得m=3.


科目:高中數學 來源: 題型:
【題目】已知命題p:“曲線C1:![]() =1表示焦點在x軸上的橢圓”,命題q:“曲線C2:
=1表示焦點在x軸上的橢圓”,命題q:“曲線C2:![]() 表示雙曲線”.
表示雙曲線”.
(1)若命題p是真命題,求m的取值范圍;
(2)若p是q的必要不充分條件,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出以下四個命題:
(1)命題![]() ,使得
,使得![]() ,則
,則![]() ,都有
,都有![]() ;
;
(2)已知函數f(x)=|log2x|,若a≠b,且f(a)=f(b),則ab=1;
(3)若平面α內存在不共線的三點到平面β的距離相等,則平面α平行于平面β;
(4)已知定義在![]() 上的函數
上的函數![]() 滿足條件
滿足條件![]() ,且函數
,且函數![]() 為奇函數,則函數
為奇函數,則函數![]() 的圖象關于點
的圖象關于點![]() 對稱.
對稱.
其中真命題的序號為______________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() .
.
(1)若直線![]() 不經過第四象限,求
不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 交
交![]() 軸負半軸于點
軸負半軸于點![]() ,交
,交![]() 軸正半軸于點
軸正半軸于點![]() ,
,![]() 為坐標原點,設
為坐標原點,設![]() 的面積為
的面積為![]() ,求
,求![]() 的最小值及此時直線
的最小值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,點
,點![]() 為橢圓
為橢圓![]() 上任意一點,
上任意一點,![]() 關于原點
關于原點![]() 的對稱點為
的對稱點為![]() ,有
,有![]() ,且
,且![]() 的最大值
的最大值![]() .
.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 是
是![]() 關于
關于![]() 軸的對稱點,設點
軸的對稱點,設點![]() ,連接
,連接![]() 與橢圓
與橢圓![]() 相交于點
相交于點![]() ,問直線
,問直線![]() 與
與![]() 軸是否交于一定點.如果是,求出該定點坐標;如果不是,說明理由.
軸是否交于一定點.如果是,求出該定點坐標;如果不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花圃為提高某品種花苗質量,開展技術創新活動,在![]() 實驗地分別用甲、乙方法培訓該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各
實驗地分別用甲、乙方法培訓該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各![]() 株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為
株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為![]() 及以上的花苗為優質花苗.
及以上的花苗為優質花苗.

![]() 求圖中
求圖中![]() 的值,并求綜合評分的中位數.
的值,并求綜合評分的中位數.
![]() 用樣本估計總體,以頻率作為概率,若在
用樣本估計總體,以頻率作為概率,若在![]() 兩塊試驗地隨機抽取
兩塊試驗地隨機抽取![]() 棵花苗,求所抽取的花苗中的優質花苗數的分布列和數學期望;
棵花苗,求所抽取的花苗中的優質花苗數的分布列和數學期望;
![]() 填寫下面的列聯表,并判斷是否有
填寫下面的列聯表,并判斷是否有![]() 的把握認為優質花苗與培育方法有關.
的把握認為優質花苗與培育方法有關.
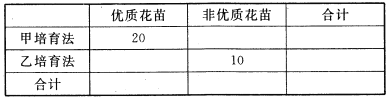
附:下面的臨界值表僅供參考.
![]()
(參考公式:![]() ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D為側棱AA1的中點.
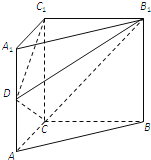
(1)求異面直線DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com