已知f(x)=x2+bx+c為偶函數,曲線y=f(x)過點(2,5),g(x)=(x+a)f(x).
(1)求曲線y=g(x)有斜率為0的切線,求實數a的取值范圍;
(2)若當x=-1時函數y=g(x)取得極值,確定y=g(x)的單調區間.
【答案】
分析:(1)據偶函數的定義f(-x)=f(x)求出b值,將點(2,5)代入得c值,據導數在切點處的導數值為切線斜率,
有g′(x)=0有實數解,由△≥0得范圍.
(2),函數在極值點處的導數值為0,導數大于0對應區間是單調遞增區間;導數小于0對應區間是單調遞減區間.
解答:解:(1)∵f(x)=x
2+bx+c為偶函數,故f(-x)=f(x)即有
(-x)
2+b(-x)+c=x
2+bx+c解得b=0
又曲線y=f(x)過點(2,5),得2
2+c=5,有c=1
∵g(x)=(x+a)f(x)=x
3+ax
2+x+a從而g′(x)=3x
2+2ax+1,
∵曲線y=g(x)有斜率為0的切線,故有g′(x)=0有實數解.即3x
2+2ax+1=0有實數解.
此時有△=4a
2-12≥0解得
a∈(-∞,-
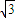
]∪[
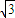
,+∞)所以實數a的取值范圍:a∈(-∞,-
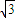
]∪[
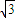
,+∞);
(2)因x=-1時函數y=g(x)取得極值,故有g′(-1)=0即3-2a+1=0,解得a=2
又g′(x)=3x
2+4x+1=(3x+1)(x+1)令g′(x)=0,得x1=-1,x2=
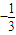
當x∈(-∞,-1)時,g′(x)>0,故g(x)在(-∞,-1)上為增函數
當
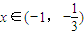
時,g′(x)<0,故g(x)在(-1,-

)上為減函數
當x∈(-
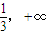
)時,g′(x)>0,故g(x)在
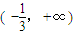
上為增函數.
點評:本題考查偶函數的定義;利用導數幾何意義求曲線切線方程;利用導數求函數單調區間.

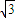 ]∪[
]∪[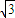 ,+∞)所以實數a的取值范圍:a∈(-∞,-
,+∞)所以實數a的取值范圍:a∈(-∞,-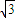 ]∪[
]∪[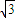 ,+∞);
,+∞);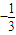
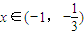 時,g′(x)<0,故g(x)在(-1,-
時,g′(x)<0,故g(x)在(-1,- )上為減函數
)上為減函數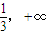 )時,g′(x)>0,故g(x)在
)時,g′(x)>0,故g(x)在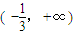 上為增函數.
上為增函數.
