
【題目】在平面直角坐標系x0y中,已知點A(﹣ ![]() ,0),B(
,0),B( ![]() ),E為動點,且直線EA與直線EB的斜率之積為﹣
),E為動點,且直線EA與直線EB的斜率之積為﹣ ![]() . (Ⅰ)求動點E的軌跡C的方程;
. (Ⅰ)求動點E的軌跡C的方程;
(Ⅱ)設過點F(1,0)的直線l與曲線C相交于不同的兩點M,N.若點P在y軸上,且|PM|=|PN|,求點P的縱坐標的取值范圍.
【答案】解:(Ⅰ)設動點E的坐標為(x,y), ∵點A(﹣ ![]() ,0),B(
,0),B( ![]() ),E為動點,且直線EA與直線EB的斜率之積為﹣
),E為動點,且直線EA與直線EB的斜率之積為﹣ ![]() ,
,
∴ ![]() ,
,
整理,得 ![]() ,x≠
,x≠ ![]() ,
,
∴動點E的軌跡C的方程為 ![]() ,x
,x ![]() .
.
(Ⅱ)當直線l的斜率不存在時,滿足條件的點P的縱坐標為0,
當直線l的斜率存在時,設直線l的方程為y=k(x﹣1),
將y=k(x﹣1)代入 ![]() ,并整理,得
,并整理,得
(2k2+1)x2﹣4k2x+2k2﹣2=0,
△=8k2+8>0,
設M(x1 , y1),N(x2 , y2),則 ![]() ,x1x2=
,x1x2= ![]() ,
,
設MN的中點為Q,則 ![]() ,
, ![]() ,
,
∴Q( ![]() ,﹣
,﹣ ![]() ),
),
由題意知k≠0,
又直線MN的垂直平分線的方程為y+ ![]() =﹣
=﹣ 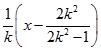 ,
,
令x=0,得yP= 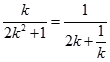 ,
,
當k>0時,∵2k+ ![]()
![]() ,∴0<
,∴0< ![]() ;
;
當k<0時,因為2k+ ![]() ≤﹣2
≤﹣2 ![]() ,所以0>yP≥﹣
,所以0>yP≥﹣ ![]() =﹣
=﹣ ![]() .
.
綜上所述,點P縱坐標的取值范圍是[﹣ ![]() ]
]
【解析】(Ⅰ)設動點E的坐標為(x,y),由點A(﹣ ![]() ,0),B(
,0),B( ![]() ),E為動點,且直線EA與直線EB的斜率之積為﹣
),E為動點,且直線EA與直線EB的斜率之積為﹣ ![]() ,知
,知 ![]() ,由此能求出動點E的軌跡C的方程.(Ⅱ)設直線l的方程為y=k(x﹣1),將y=k(x﹣1)代入
,由此能求出動點E的軌跡C的方程.(Ⅱ)設直線l的方程為y=k(x﹣1),將y=k(x﹣1)代入 ![]() ,得(2k2+1)x2﹣4k2x+2k2﹣2=0,由題設條件能推導出直線MN的垂直平分線的方程為y+
,得(2k2+1)x2﹣4k2x+2k2﹣2=0,由題設條件能推導出直線MN的垂直平分線的方程為y+ ![]() =﹣
=﹣ ![]() ,由此能求出點P縱坐標的取值范圍.
,由此能求出點P縱坐標的取值范圍.


 習題精選系列答案
習題精選系列答案科目:高中數(shù)學 來源: 題型:
【題目】平面α過正方體ABCD﹣A1B1C1D1的頂點A,α∥平面CB1D1 , α∩平面ABCD=m,α∩平面ABB1A1=n,則m、n所成角的正弦值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() ,(x>0且a≠1)的圖象經(jīng)過點(﹣2,3).
,(x>0且a≠1)的圖象經(jīng)過點(﹣2,3). 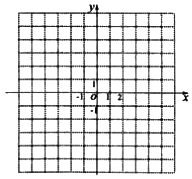
(Ⅰ)求a的值,并在給出的直角坐標系中畫出y=f(x)的圖象;
(Ⅱ)若f(x)在區(qū)間(m,m+1)上是單調函數(shù),求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD ![]() ,M為棱PB的中點. (Ⅰ)證明:DM⊥平面PBC;
,M為棱PB的中點. (Ⅰ)證明:DM⊥平面PBC;
(Ⅱ)求二面角A﹣DM﹣C的余弦值.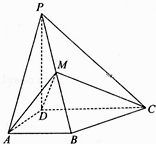
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,三角形ABC為等腰直角三角形,AC=BC= ![]() ,AA1=1,點D是AB的中點.
,AA1=1,點D是AB的中點. 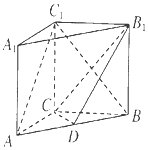
(1)求證:AC1∥平面CDB1;
(2)二面角B1﹣CD﹣B的平面角的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1,已知長方形ABCD中,AB=2,AD=1,E為DC的中點.將△ADE沿AE折起,使得平面ADE⊥平面ABCE. 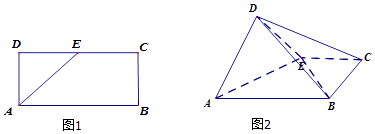
(1)求證:平面BDE⊥平面ADE
(2)求三棱錐 C﹣BDE的體積
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義域為R的函數(shù)f(x)= ![]() 是奇函數(shù).
是奇函數(shù).
(1)求實數(shù)a的值,并判斷f(x)的單調性(不用證明);
(2)已知不等式f(logm ![]() )+f(﹣1)>0恒成立,求實數(shù)m的取值范圍.
)+f(﹣1)>0恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】關于函數(shù) ![]() ,看下面四個結論( )
,看下面四個結論( )
①f(x)是奇函數(shù);②當x>2007時, ![]() 恒成立;③f(x)的最大值是
恒成立;③f(x)的最大值是 ![]() ;④f(x)的最小值是
;④f(x)的最小值是 ![]() .其中正確結論的個數(shù)為:
.其中正確結論的個數(shù)為:
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com