
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的中心為原點,焦點
的中心為原點,焦點![]() ,
,![]() 在
在![]() 軸上,離心率為
軸上,離心率為![]() .過
.過![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)圓![]() 與
與![]() 軸正半軸相交于兩點
軸正半軸相交于兩點![]() ,
,![]() (點
(點![]() 在點
在點![]() 的左側),過點
的左側),過點![]() 任作一條直線與橢圓
任作一條直線與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,連接
兩點,連接![]() ,
,![]() ,求證
,求證![]() .
.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】
(1)設橢圓C的方程為![]() (a>b>0),由離心率為
(a>b>0),由離心率為![]() ,得
,得![]() ,又△PQF2的周長為4a=
,又△PQF2的周長為4a=![]() ,得a=2
,得a=2![]() ,進而求出橢圓方程;
,進而求出橢圓方程;
(2)把y=0代入圓的方程求出x的值,確定M與N的坐標,當AB⊥x軸時,由橢圓的對稱性得證;當AB與x軸不垂直時,設直線AB為y=k(x﹣1),與橢圓方程聯立得到關于x的一元二次方程,設A(x1,y1),B(x2,y2),利用韋達定理表示出x1+x2,x1x2,進而表示出直線AN與直線BN斜率之和為0,即可得證.
(1)設橢圓C的方程為![]() (a>b>0).因為離心率為
(a>b>0).因為離心率為![]() ,所以
,所以![]() ,解得
,解得![]() ,即
,即![]() .又△PQF2的周長為|PQ|+|PF2|+|QF2|=(|PF1|+|PF2|)+(|QF1|+|QF2|)=2a+2a=4a,所以又△PQF2的周長為,即a=2
.又△PQF2的周長為|PQ|+|PF2|+|QF2|=(|PF1|+|PF2|)+(|QF1|+|QF2|)=2a+2a=4a,所以又△PQF2的周長為,即a=2![]() ,b=2,
,b=2,
所以橢圓C的方程為![]() .
.
(2)把y=0代入![]() +(y-2)2=
+(y-2)2=![]() ,解得x=1或x=4,因為點
,解得x=1或x=4,因為點![]() 在點
在點![]() 的左側,即點M(1,0),N(4,0).
的左側,即點M(1,0),N(4,0).
①當AB⊥x軸時,由橢圓的對稱性可知∠ANM=∠BNM.
②當AB與x軸不垂直時,可設直線AB的方程為y=k(x-1).
聯立![]() (k2+2)x2-2k2x+k2-8=0.
(k2+2)x2-2k2x+k2-8=0.
設A(x1,y1),B(x2,y2),
則x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
因為y1=k(x1-1),y2=k(x2-1),
所以kAN+kBN=![]() +
+![]() =
=![]() +
+![]() =
=![]() .
.
因為(x1-1)(x2-4)+(x2-1)(x1-4)=2x1x2-5(x1+x2)+8=![]() +8=
+8=![]() ,
,
所以kAN+kBN=0,所以∠ANM=∠BNM,綜上所述,∠ANM=∠BNM.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數且
為參數且 ![]() )曲線
)曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,且
為參數,且![]() ),以
),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 與
與![]() 的交點到極點的距離;
的交點到極點的距離;
(2)設![]() 與
與![]() 交于
交于![]() 點,
點,![]() 與
與![]() 交于
交于![]() 點,當
點,當![]() 在
在![]() 上變化時,求
上變化時,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
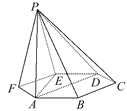
【題目】如圖,已知六棱錐P-ABCDEF的底面是正六邊形,PA⊥平面ABC,PA=2AB,則下列結論中:①PB⊥AE;②平面ABC⊥平面PBC;③直線BC∥平面PAE;④∠PDA=45°.
其中正確的有____________(把所有正確的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來大氣污染防治工作得到各級部門的重視,某企業在現有設備下每日生產總成本![]() (單位:萬元)與日產量
(單位:萬元)與日產量![]() (單位:噸)之間的函數關系式為
(單位:噸)之間的函數關系式為![]() ,現為了配合環境衛生綜合整治,該企業引進了除塵設備,每噸產品除塵費用為
,現為了配合環境衛生綜合整治,該企業引進了除塵設備,每噸產品除塵費用為![]() 萬元,除塵后當日產量
萬元,除塵后當日產量![]() 時,總成本
時,總成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每噸產品出廠價為48萬元,試求除塵后日產量為多少時,每噸產品的利潤最大,最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,兩焦點分別為雙曲線
的中心在坐標原點,兩焦點分別為雙曲線![]() 的頂點,直線
的頂點,直線![]() 與橢圓
與橢圓![]() 交于A,B兩點,且點A的坐標為
交于A,B兩點,且點A的坐標為![]() ,點Р是橢圓
,點Р是橢圓![]() 上異于A,B的任意一點,點Q滿足
上異于A,B的任意一點,點Q滿足![]() ,
,![]() ,且A,B,Q三點不共線.
,且A,B,Q三點不共線.
(1)求橢圓![]() 的方程;
的方程;
(2)求點Q的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com