
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
,![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() ,
,![]() .
.
(1)若![]() 為等邊三角形,求橢圓
為等邊三角形,求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的短軸長為2,過點
的短軸長為2,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
試題分析:(1)由![]() 為等邊三角形可得a=2b,又c=1,集合
為等邊三角形可得a=2b,又c=1,集合![]() 可求
可求![]() ,則橢圓C的方程可求;(2)由給出的橢圓C的短軸長為2,結合c=1求出橢圓方程,分過點F2的直線l的斜率存在和不存在討論,當斜率存在時,把直線方程和橢圓方程聯立,由根與系數關系寫出兩個交點的橫坐標的和,把
,則橢圓C的方程可求;(2)由給出的橢圓C的短軸長為2,結合c=1求出橢圓方程,分過點F2的直線l的斜率存在和不存在討論,當斜率存在時,把直線方程和橢圓方程聯立,由根與系數關系寫出兩個交點的橫坐標的和,把
![]() 轉化為數量積等于0,代入坐標后可求直線的斜率,則直線l的方程可求
轉化為數量積等于0,代入坐標后可求直線的斜率,則直線l的方程可求
試題解析:(1)![]() 為等邊三角形,則
為等邊三角形,則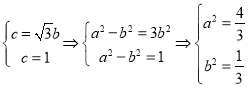 ……2
……2
橢圓![]() 的方程為:
的方程為:![]() ; ……3
; ……3
(2)容易求得橢圓![]() 的方程為
的方程為![]() , ……5
, ……5
當直線![]() 的斜率不存在時,其方程為
的斜率不存在時,其方程為![]() ,不符合題意; ……6
,不符合題意; ……6
當直線的斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,
由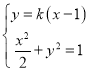 得
得![]() ,設
,設![]() ,
,
則![]() , ……8
, ……8
![]() ∵
∵![]() ,
,
∴![]() ,
,
即![]()
![]() ……10
……10
解得![]() ,即
,即![]() ,
,
故直線![]() 的方程為
的方程為![]() 或
或![]() . ……12
. ……12


科目:高中數學 來源: 題型:
【題目】某科研機構研發了某種高新科技產品,現已進入實驗階段.已知實驗的啟動資金為10萬元,從實驗的第一天起連續實驗,第![]() 天的實驗需投入實驗費用為
天的實驗需投入實驗費用為![]() 元
元![]() ,實驗30天共投入實驗費用17700元.
,實驗30天共投入實驗費用17700元.
(1)求![]() 的值及平均每天耗資最少時實驗的天數;
的值及平均每天耗資最少時實驗的天數;
(2)現有某知名企業對該項實驗進行贊助,實驗![]() 天共贊助
天共贊助![]() 元
元![]() .為了保證產品質量,至少需進行50天實驗,若要求在平均每天實際耗資最小時結束實驗,求
.為了保證產品質量,至少需進行50天實驗,若要求在平均每天實際耗資最小時結束實驗,求![]() 的取值范圍.(實際耗資=啟動資金+試驗費用-贊助費)
的取值范圍.(實際耗資=啟動資金+試驗費用-贊助費)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記![]() 表示
表示![]() 中的最大值,如
中的最大值,如![]() ,已知函數
,已知函數![]() .
.
(1)求函數![]() 在
在![]() 上的值域;
上的值域;
(2)試探討是否存在實數![]() , 使得
, 使得![]() 對
對![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范圍;
的取值范圍;
若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,cos C=.
(1)若·=,求c的最小值;
(2)設向量x=(2sin B,-),y=,且x∥y,求sin(B-A)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為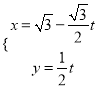 (
(![]() 為參數),以原點為極點,
為參數),以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,
, ![]() ,若
,若![]() 的中點為
的中點為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com