Question

【題目】已知函數(shù)f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π，x∈R）在一個周期內(nèi)的圖象如圖所示，則函數(shù)的解析式為 ． 直線y= 與函數(shù)y=f（x）（x∈R）圖象的所有交點的坐標為 ．

Answer 1

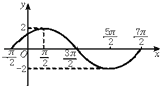
【答案】f（x）=2sin（ x+ ）；（ +4kπ， ）或（ +4kπ， ）（k∈Z）
【解析】解：∵f（x）=Asin（ωx+φ）（A＞0，ω＞0，x∈R），
∴A=2，周期T= = ﹣（﹣ ）=4π，
∴ω= ．
∴f（x）=2sin（ x+φ），
又f（﹣ ）=2sin（ ×（﹣ ）+φ）=0，
∴φ﹣ =kπ，k∈Z，|φ|＜π，
∴φ= ．
∴f（x）=2sin（ x+ ）．
當f（x）= 時，即2sin（ x+ ）= ，可得sin（ x+ ）= ，
∴ x+ = +2kπ或 x+ = +2kπ（k∈Z），可得x= +4kπ或 +4kπ（k∈Z）
由此可得，直線y= 與函數(shù)f（x）圖象的所有交點的坐標為：（ +4kπ， ）或（ +4kπ， ）（k∈Z）．
所以答案是：f（x）=2sin（ x+ ），（ +4kπ， ）或（ +4kπ， ）（k∈Z）．