
已知直線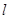 的參數(shù)方程為
的參數(shù)方程為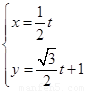 (t為參數(shù)),曲線C的參數(shù)方程為
(t為參數(shù)),曲線C的參數(shù)方程為
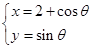 (
(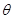 為參數(shù)).
為參數(shù)).
(1)已知在極坐標(biāo)系(與直角坐標(biāo)系xOy取相同的長度單位,且以原點(diǎn)O為極點(diǎn),以x軸正半軸為極軸)中,點(diǎn)P的極坐標(biāo)為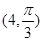 ,判斷點(diǎn)P與直線
,判斷點(diǎn)P與直線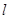 的位置關(guān)系;
的位置關(guān)系;
(2)設(shè)點(diǎn)Q是曲線C上的一個(gè)動(dòng)點(diǎn),求點(diǎn)Q到直線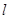 的距離的最小值與最大值.
的距離的最小值與最大值.
(1) 不在直線
不在直線 上;(2)最小值為
上;(2)最小值為 ,最大值為
,最大值為 .
.
【解析】
試題分析:(1)消去參數(shù),將直線的參數(shù)方程化為普通方程,利用 ,再將點(diǎn)
,再將點(diǎn) 的極坐標(biāo)化為直角坐標(biāo),再判斷點(diǎn)
的極坐標(biāo)化為直角坐標(biāo),再判斷點(diǎn) 的坐標(biāo)是否滿足方程,進(jìn)而判斷點(diǎn)和直線的位置關(guān)系;(2)設(shè)點(diǎn)
的坐標(biāo)是否滿足方程,進(jìn)而判斷點(diǎn)和直線的位置關(guān)系;(2)設(shè)點(diǎn) ,利用點(diǎn)到直線的距離公式表示點(diǎn)Q到直線
,利用點(diǎn)到直線的距離公式表示點(diǎn)Q到直線 的距離
的距離 ,轉(zhuǎn)化為三角函數(shù)的最值問題處理.
,轉(zhuǎn)化為三角函數(shù)的最值問題處理.
試題解析:(Ⅰ)將點(diǎn)
 化為直角坐標(biāo),得
化為直角坐標(biāo),得 ,直線
,直線 的普通方程為
的普通方程為 ,顯然點(diǎn)
,顯然點(diǎn) 不滿足直線
不滿足直線 的方程,所以點(diǎn)
的方程,所以點(diǎn) 不在直線
不在直線 上.
上.
(Ⅱ)因?yàn)辄c(diǎn) 在曲線
在曲線 上,故可設(shè)點(diǎn)
上,故可設(shè)點(diǎn) ,點(diǎn)
,點(diǎn) 到直線
到直線 :
: 的距離為
的距離為
 ,所以當(dāng)
,所以當(dāng) 時(shí),
時(shí), ,
,
當(dāng) 時(shí),
時(shí), .故點(diǎn)
.故點(diǎn) 到直線
到直線 的距離的最小值為
的距離的最小值為 ,最大值為
,最大值為 .
.
考點(diǎn):1直線參數(shù)方程和普通方程的互化;2、極坐標(biāo)和直角坐標(biāo)的互化;3、點(diǎn)到直線的距離.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年山東省微山一中高二下學(xué)期期末考試數(shù)學(xué)(理) 題型:解答題
已知直線 的參數(shù)方程為
的參數(shù)方程為 (t為參數(shù)),曲線C的極坐標(biāo)方程是
(t為參數(shù)),曲線C的極坐標(biāo)方程是 以極點(diǎn)為原點(diǎn),極軸為x軸正方向建立直角坐標(biāo)系,點(diǎn)
以極點(diǎn)為原點(diǎn),極軸為x軸正方向建立直角坐標(biāo)系,點(diǎn) ,直線
,直線 與曲
與曲
線C交于A,B兩點(diǎn).
(1)寫出直線 的普通方程與曲線C的直角坐標(biāo)方程;
的普通方程與曲線C的直角坐標(biāo)方程;
(2)線段MA,MB長度分別記|MA|,|MB|,求|MA|·|MB|的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆河北唐山市高三年級摸底考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
極坐標(biāo)系與直角坐標(biāo)系 有相同的長度單位,以原點(diǎn)
有相同的長度單位,以原點(diǎn) 為極點(diǎn),以
為極點(diǎn),以 軸正半軸為極軸.已知直線
軸正半軸為極軸.已知直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),曲線
為參數(shù)),曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .
.
(Ⅰ)求 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)直線 與曲線
與曲線 交于
交于 兩點(diǎn),求弦長
兩點(diǎn),求弦長 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆遼寧省分校高二下學(xué)期期中考試文科數(shù)學(xué)試卷(解析版) 題型:填空題
已知直線 的參數(shù)方程為:
的參數(shù)方程為: (
( 為參數(shù)),圓
為參數(shù)),圓 的極坐標(biāo)方程為
的極坐標(biāo)方程為  ,則直線
,則直線 與圓
與圓 的位置關(guān)系為
的位置關(guān)系為
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com