【題目】已知⊙H被直線x-y-1=0,x+y-3=0分成面積相等的四個部分,且截x軸所得線段的長為2。
(I)求⊙H的方程;
(Ⅱ)若存在過點P(0,b)的直線與⊙H相交于M，N兩點,且點M恰好是線段PN的中點,求實數b的取值范圍
【答案】（1）
（2）
【解析】試題分析：（I）設
的方程為
，由題意可知圓心
一定是兩直線
的交點，可得交點為
，所以
. 又
截x軸所得線段的長為2，所以
.，即可得到⊙H的方程;
（II）法一：如圖， 
的圓心
，半徑
，
過點N作
的直徑
，連結
.
由題可得“點
是線段
的中點”等價于“圓上存在一點
使得
的長等于
的直徑”.
由此得到實數b的取值范圍
法二：如圖， 
的圓心
，半徑
，連結
，
過
作
交
于點
，并設
.
由題意得
，所以
，
又因為
，所以
，由此得到實數b的取值范圍
試題解析：（I）設
的方程為
，
因為
被直線
分成面積相等的四部分，
所以圓心
一定是兩直線
的交點，
易得交點為
，所以
.
又
截x軸所得線段的長為2，所以
.
所以
的方程為
.
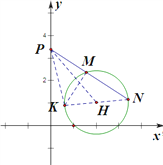
（II）法一：如圖， 
的圓心
，半徑
，
過點N作
的直徑
，連結
.
當
與
不重合時， 
，
又點
是線段
的中點
；
當
與
重合時，上述結論仍成立.
因此，“點
是線段
的中點”等價于“圓上存在一點
使得
的長等于
的直徑”.
由圖可知
，即
，即
.
顯然
，所以只需
，即
，解得
.
所以實數
的取值范圍是
.
法二：如圖， 
的圓心
，半徑
，連結
，
過
作
交
于點
，并設
.
由題意得
，
所以
，
又因為
，所以
，
將
代入整理可得
，
因為
，所以
，，解得
.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案
目標測試系列答案科目：高中數學 來源： 題型：
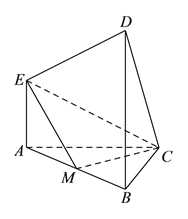
【題目】在如圖所示的多面體中， 
平面
， 
平面
， 
，且
， 
是
的中點．
（Ⅰ）求證： 
．
（Ⅱ）求平面
與平面
所成的銳二面角的余弦值．
（Ⅲ）在棱
上是否存在一點
，使得直線
與平面
所成的角是
．若存在，指出點
的位置；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
，直線
過拋物線焦點，且與拋物線交于
， 
兩點，以線段
為直徑的圓與拋物線準線的位置關系是（ ）
A. 相離 B. 相交 C. 相切 D. 不確定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f(x)＝a(x－5)2＋6lnx，其中a∈R，曲線y＝f(x)在點(1，f(1))處的切線與y軸相交于點(0,6)．
(1)確定a的值；
(2)求函數f(x)的單調區間與極值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廣場有一塊不規則的綠地如圖所示，城建部門欲在該地上建造一個底座為三角形的環境標志，小李，小王設計的底座形狀分別為
， 
，經測量
米， 
米， 
米， 
（I）求
的長度；
（Ⅱ）若環境標志的底座每平方米造價為
元，不考慮其他因素，小李，小王誰的設計建造費用最低（請說明理由），最低造價為多少？（
）
查看答案和解析>>
科目：高中數學 來源： 題型：
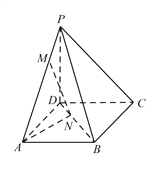
【題目】如圖，四棱錐
中，底面
為平行四邊形， 
， 
是棱PD的中點，且
， 
．
（I）求證： 
； （Ⅱ）求二面角
的大小；
（Ⅲ）若
是
上一點，且直線
與平面
成角的正弦值為
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2016年9月3日,抗戰勝利71周年紀念活動在北京隆重舉行，受到全國人民的矚目.紀念活動包括舉行紀念大會、閱兵式、擁待會和文藝晚會等，據統計，抗戰老兵由于身體原因，參加紀念大會、閱兵式、招待會這個環節(可參加多個，也可都不參加)的情況及其概率如下表所示:
(Ⅰ)若m=2n，則從這60名抗戰老兵中按照參加紀念活動的環節數分層抽取6人進行座談,求從參加紀念活動環節數為1的抗戰老兵中抽取的人數；
(Ⅱ)某醫療部門決定從(Ⅰ)中抽取的6名抗戰老兵中隨機抽取2名進行體檢,求這2名抗戰老兵中至少有1人參加紀念活動的環節數為3的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐 
底面為正方形，已知 
，
，點 
為線段 
上任意一點（不含端點），點 
在線段 
上，且 
．
（1）求證：
；
（2）若 為線段 中點，求直線 
與平面 
所成的角的余弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
