
【題目】平面上有7個點,每三點的兩兩連線都組成一個不等邊三角形.求證:一定可以找到4對三角形,使每對三角形的公共邊既是其中一個三角形的最長邊又是另一個三角形的最短邊.
【答案】見解析
【解析】
記平面上的7個點為![]() ,
,![]() ,…,
,…,![]() .因為每三點兩兩連線都組成不等邊三角形,故每個三角形都有最長邊,也都有最短邊.現將每個三角形的最長邊都染上紅色,剩下的邊染上藍色,則每一個三角形都有紅色邊.
.因為每三點兩兩連線都組成不等邊三角形,故每個三角形都有最長邊,也都有最短邊.現將每個三角形的最長邊都染上紅色,剩下的邊染上藍色,則每一個三角形都有紅色邊.
下面證明:![]() 個三角形中必有4個同色三角形.
個三角形中必有4個同色三角形.
(1)6階完全圖的邊作二染色,至少有2個同色三角形.
設![]() 的引線中有
的引線中有![]() 條紅線,
條紅線,![]() 條藍線,以
條藍線,以![]() 為頂點的非同色三角形有
為頂點的非同色三角形有![]() 個.
個.
由![]() ,知
,知![]() .
.
則非同色三角形總計為![]() .
.
故同色三角形的個數![]() 應滿足
應滿足![]() .
.
(2)7階完全圖的邊作二染色,至少有4個同色三角形.
由(1)的證明知,此時,至少有2個同色三角形.不妨設其中一個為![]() ,去掉
,去掉![]() ,對剩下的6個點又應有2個同色三角形,且異于
,對剩下的6個點又應有2個同色三角形,且異于![]() ,這就得到3個同色三角形.
,這就得到3個同色三角形.
這3個同色三角形有9個頂點,取自7個不同的點,故至少有2個頂點重合于某一![]() ,去掉
,去掉![]() ,則去掉了2個同色三角形,剩下的6個點又應有2個同色三角形,它們與被去掉的2個同色三角形是不相同的,故一共有4個不同的同色三角形.
,則去掉了2個同色三角形,剩下的6個點又應有2個同色三角形,它們與被去掉的2個同色三角形是不相同的,故一共有4個不同的同色三角形.
(3)由于每一個三角形都有紅邊,這4個同色三角形必為紅色三角形,每個紅色三角形的最短邊必為另一個三角形的最長邊.這就找到了4條連線(每個紅色三角形的最短邊,即使是兩個紅色三角形的公共邊也沒有關系),每一條既是一個三角形的最長邊(紅色),又是另一個三角形(所在紅色三角形)的最短邊.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體![]() 中,底面
中,底面![]() 為菱形,
為菱形, ![]() ,
, ![]() ,
, ![]() 與
與![]() 相交于
相交于![]() 點,四邊形
點,四邊形![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.
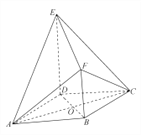
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生產基地有五臺機器,現有五項工作待完成,每臺機器完成每項工作后獲得的效益值如表所示.若每臺機器只完成一項工作,且完成五項工作后獲得的效益值總和最大,則下列敘述錯誤的的是_____________.
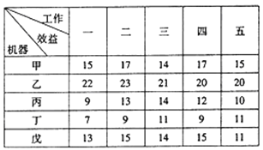
①甲只能承擔第四項工作
②乙不能承擔第二項工作
③丙可以不承擔第三項工作
④丁可以承擔第三項工作
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 、
、![]() 為大于3的整數,將
為大于3的整數,將![]() 的立方體分割為
的立方體分割為![]() 個單位正方體,從一角的單位正方體起第
個單位正方體,從一角的單位正方體起第![]() 層、第
層、第![]() 行、第
行、第![]() 列的單位正方體記為
列的單位正方體記為![]() .求所有有序六元數組
.求所有有序六元數組![]() 的個數,使得一只螞蟻從
的個數,使得一只螞蟻從![]() 出發,經過每個小正方體恰一次到達
出發,經過每個小正方體恰一次到達![]() .(注)螞蟻可以從一個單位正方體爬到另一個與之有公共面的相鄰正方體.
.(注)螞蟻可以從一個單位正方體爬到另一個與之有公共面的相鄰正方體.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線![]() 的焦點
的焦點![]() 作直線
作直線![]() 與拋物線交于點
與拋物線交于點![]() 、
、![]() .
.
(1)求證:![]() 不是直角三角形.
不是直角三角形.
(2)當![]() 的斜率為
的斜率為![]() 時,拋物線上是否存在點
時,拋物線上是否存在點![]() ,使
,使![]() 為直角三角形?若存在,求出所有的點
為直角三角形?若存在,求出所有的點![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農歷戊戌年即將結束,為了迎接新年,小康、小梁、小譚、小劉、小林每人寫了一張心愿卡,設計了一個與此心愿卡對應的漂流瓶.現每人隨機的選擇一個漂流瓶將心愿卡放入,則事件“至少有兩張心愿卡放入對應的漂流瓶”的概率為___
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)=![]() ,
,
(1)求f(x)的最小值;
(2)對任意![]() ,
,![]() 都有恒成立,求實數a的取值范圍;
都有恒成立,求實數a的取值范圍;
(3)證明:對一切![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點
的兩個焦點![]() ,
,![]() 與短軸的一個端點構成一個等邊三角形,且直線
與短軸的一個端點構成一個等邊三角形,且直線![]() 與圓
與圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)已知過橢圓![]() 的左頂點
的左頂點![]() 的兩條直線
的兩條直線![]() ,
,![]() 分別交橢圓
分別交橢圓![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() ,求證:直線
,求證:直線![]() 過定點,并求出定點坐標;
過定點,并求出定點坐標;
(3)在(2)的條件下求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com