【題目】高斯是德國著名的數學家，近代數學奠基者之一，享有“數學王子”的稱號，他和阿基米德、牛頓并列為世界三大數學家，用其名字命名的“高斯函數”為：設
，用
表示不超過x的最大整數，則
稱為高斯函數，例如：
，
.已知函數
，則關于函數
的敘述中正確的是（ ）
A.
是偶函數B.
是奇函數
C.在R上是增函數D.的值域是
E.的值域是
長江作業本同步練習冊系列答案科目：高中數學 來源： 題型：
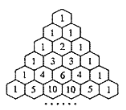
【題目】“楊輝三角”是我國數學史上的一個偉大成就，是二項式系數在三角形中的一種幾何排列.如圖所示，去除所有為1的項，依此構成數列2，3，3，4，6，4，5，10，10，5，…，則此數列的前46項和為_____.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】大型綜藝節目《最強大腦》中，有一個游戲叫做盲擰魔方，就是玩家先觀察魔方狀態并進行記憶，記住后蒙住眼睛快速還原魔方．根據調查顯示，是否喜歡盲擰魔方與性別有關．為了驗證這個結論，某興趣小組隨機抽取了100名魔方愛好者進行調查，得到的部分數據如表所示：已知在全部100人中隨機抽取1人抽到喜歡盲擰的概率為
．
喜歡盲擰 | 不喜歡盲擰 | 總計 | |
男 | 10 | ||
女 | 20 | ||
總計 | 100 |
表（1）
并邀請這100人中的喜歡盲擰的人參加盲擰三階魔方比賽，其完成時間的頻率分布如表所示：
完成時間（分鐘） | [0，10） | [10，20） | [20，30） | [30，40] |
頻率 | 0.2 | 0.4 | 0.3 | 0.1 |
表（2）
（Ⅰ）將表（1）補充完整，并判斷能否在犯錯誤的概率不超過0.001的前提下認為是否喜歡盲擰與性別有關？
（Ⅱ）現從表（2）中完成時間在[30，40] 內的人中任意抽取2人對他們的盲擰情況進行視頻記錄，記完成時間在[30，40]內的甲、乙、丙3人中恰有一人被抽到為事件A，求事件A發生的概率．
（參考公式：
，其中
）
P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知m、n是不重合的直線，α、β是不重合的平面，有下列命題：①若m
α，n∥α，則m∥n；②若m∥α，m∥β，則α∥β；③若α∩β=n，m∥n，則m∥α且m∥β；④若m⊥α，m⊥β，則α∥β.其中真命題的個數是（ ）
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某次詩詞大會決賽前，甲、乙、丙丁四位選手有機會問鼎冠軍，
三名詩詞愛好者依據選手在之前比賽中的表現，結合自己的判斷，對本場比賽的冠軍進行了如下猜測：
猜測冠軍是乙或丁；
猜測冠軍一定不是丙和丁；
猜測冠軍是甲或乙。比賽結束后發現，三個人中只有一個人的猜測是正確的，則冠軍是（ ）
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，以坐標原點
為極點，以
軸正半軸為極軸，建立極坐標系，已知直線
的參數方程為
（
為參數），曲線
的極坐標方程為
.
(1)求曲線的直角坐標方程，并指出該曲線是什么曲線；
(2)若直線 與曲線的交點分別為
，求
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
