
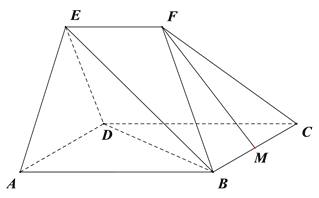
【題目】如圖,在幾何體![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為菱形,且
為菱形,且![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 為
為![]() 中點.
中點.
(Ⅰ)求證: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使
,使![]()
![]() ? 若存在,求
? 若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1)見解析(2)![]() (3)
(3)![]()
【解析】試題分析:(Ⅰ)取![]() 中點
中點![]() ,連結
,連結![]() ,利用面面平行平面
,利用面面平行平面![]() ∥平面
∥平面![]() ,得到線面平行
,得到線面平行![]() ∥平面
∥平面![]() ;(Ⅱ)取
;(Ⅱ)取![]() 中點
中點![]() ,連結
,連結![]() ,
, ![]() ,先證
,先證![]() 兩兩垂直,故可以
兩兩垂直,故可以![]() 為原點,
為原點, ![]() 為
為![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() ,求出
,求出![]() 的方向向量
的方向向量![]() ,面
,面![]() 的法向量
的法向量![]() ,利用
,利用![]() 可得結果;(Ⅲ)設
可得結果;(Ⅲ)設![]() 是
是![]() 上一點,且
上一點,且![]() ,根據共線可得
,根據共線可得![]() 的坐標,結合數量積為0,可得結果.
的坐標,結合數量積為0,可得結果.
試題解析:(Ⅰ)

取![]() 中點
中點![]() ,連結
,連結![]() .
.
因為![]() 分別為
分別為![]() 中點,所以
中點,所以![]() ∥
∥![]() .
.
又![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
因為![]() ∥
∥![]() ,
, ![]() ,所以
,所以![]() ∥
∥![]() ,
, ![]() .
.
所以四邊形![]() 為平行四邊形.所以
為平行四邊形.所以![]() ∥
∥![]() .
.
又![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
又![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
(Ⅱ)

取![]() 中點
中點![]() ,連結
,連結![]() ,
, ![]() .因為
.因為![]() ,所以
,所以![]() .
.
因為平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]() .
.
因為![]() ,
, ![]() ,所以△
,所以△![]() 為等邊三角形.
為等邊三角形.
因為![]() 為
為![]() 中點,所以
中點,所以![]() .
.
因為![]() 兩兩垂直,設
兩兩垂直,設![]() ,以
,以![]() 為原點,
為原點, ![]()
![]() 軸,如圖建立空間直角坐標系
軸,如圖建立空間直角坐標系![]() ,由題意得,
,由題意得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則
,則 即
即
令![]() ,則
,則![]() ,
, ![]() .所以
.所以![]() .
.
設直線![]() 與平面
與平面![]() 成角為
成角為![]() ,
, ![]()
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
(Ⅲ)設![]() 是
是![]() 上一點,且
上一點,且![]() ,
, ![]() ,因此點
,因此點![]() .
.
![]() .由
.由![]() ,解得
,解得![]() .
.
所以在棱![]() 上存在點
上存在點![]() 使得
使得![]()
![]() ,此時
,此時![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() 是自然對數的底數.
是自然對數的底數.
(Ⅰ)判斷函數![]() 在
在![]() 內零點的個數,并說明理由;
內零點的個數,并說明理由;
(Ⅱ)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,試求實數
成立,試求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明計劃在8月11日至8月20日期間游覽某主題公園.根據旅游局統計數據,該主題公園在此期間“游覽舒適度”(即在園人數與景區主管部門核定的最大瞬時容量之比,40%以下為舒適,40%—60%為一般,60%以上為擁擠)情況如圖所示.小明隨機選擇8月11日至8月19日中的某一天到達該主題公園,并游覽2天.
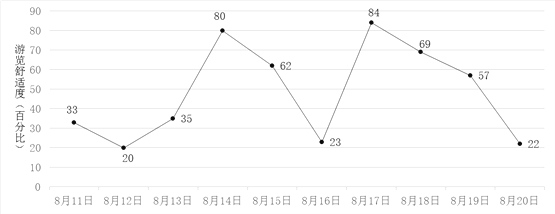 (Ⅰ)求小明連續兩天都遇上擁擠的概率;
(Ⅰ)求小明連續兩天都遇上擁擠的概率;
(Ⅱ)設![]() 是小明游覽期間遇上舒適的天數,求
是小明游覽期間遇上舒適的天數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)由圖判斷從哪天開始連續三天游覽舒適度的方差最大?(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
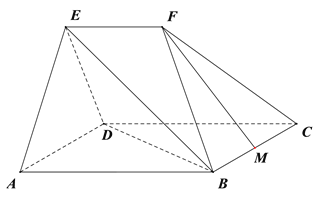
【題目】如圖,在幾何體![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為菱形,且
為菱形,且![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 為
為![]() 中點.
中點.
(Ⅰ)求證: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使
,使![]()
![]() ? 若存在,求
? 若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,a1=2,an+1=4an﹣3n+1,n∈N* .
(1)證明數列{an﹣n}是等比數列;
(2)求數列{an}的前n項和Sn;
(3)證明不等式Sn+1≤4Sn , 對任意n∈N*皆成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,點
,點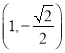 是橢圓
是橢圓![]() 上的點,離心率為
上的點,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)點![]() 在橢圓上
在橢圓上![]() 上,若點
上,若點![]() 與點
與點![]() 關于原點的對稱,連接
關于原點的對稱,連接![]() ,并延長與橢圓
,并延長與橢圓![]() 的另一個交點為
的另一個交點為![]() ,連接
,連接![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知非零向量 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 滿足
滿足 ![]() =2
=2 ![]() ﹣
﹣ ![]() ,
, ![]() =k
=k ![]() +
+ ![]() ,給出以下結論:
,給出以下結論:
①若 ![]() 與
與 ![]() 不共線,
不共線, ![]() 與
與 ![]() 共線,則k=﹣2;
共線,則k=﹣2;
②若 ![]() 與
與 ![]() 不共線,
不共線, ![]() 與
與 ![]() 共線,則k=2;
共線,則k=2;
③存在實數k,使得 ![]() 與
與 ![]() 不共線,
不共線, ![]() 與
與 ![]() 共線;
共線;
④不存在實數k,使得 ![]() 與
與 ![]() 不共線,
不共線, ![]() 與
與 ![]() 共線.
共線.
其中正確結論的個數是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+(y﹣1)2=5,直線l:mx﹣y+1﹣m=0,且直線l與圓C交于A、B兩點.
(1)若|AB|= ![]() ,求直線l的傾斜角;
,求直線l的傾斜角;
(2)若點P(1,1),滿足2 ![]() =
= ![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中有四個小球,分別寫有“幸”“福”“快”“樂”四個字,有放回地從中任取一個小球,取到“快”就停止,用隨機模擬的方法估計直到第二次停止的概率:先由計算器產生1到4之間取整數值的隨機數,且用1,2,3,4表示取出小球上分別寫有“幸”“福”“快”“樂”四個字,以每兩個隨機數為一組,代表兩次的結果,經隨機模擬產生了20組隨機數:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
據此估計,直到第二次就停止的概率為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com